Example for Gauss-Newton method

Contents

Define function f(x) and Jacobian f'(x)

Here we use @-functions in Matlab. For more complicated functions one can define the functions in separate m-files f.m and fp.m .

f = @(x) [x(1)-1; x(2)-2 ; x(1)^2+x(2)^2-3];
fp = @(x) [ 1, 0 ; 0, 1; 2*x(1), 2*x(2) ];

Plot zero contours of the functions f1, f2, f3

h = ezplot('1*x1+0*x2-1',[-3 3 -3 3]); hold on  % plot curves where f1=0
set(h,'LineColor','r');                         % and make this red
h = ezplot('0*x1+1*x2-2',[-3 3 -3 3]);          % plot curves where f2=0
set(h,'LineColor','g');                         % and make this green
h = ezplot('x1^2+x2^2-3',[-3 3 -3 3]);          % plot curves where f3=0
set(h,'LineColor','b');                         % and make this blue
title('zero contours of f1,f2,f3')
axis equal
legend('f1=0','f2=0','f3=0')

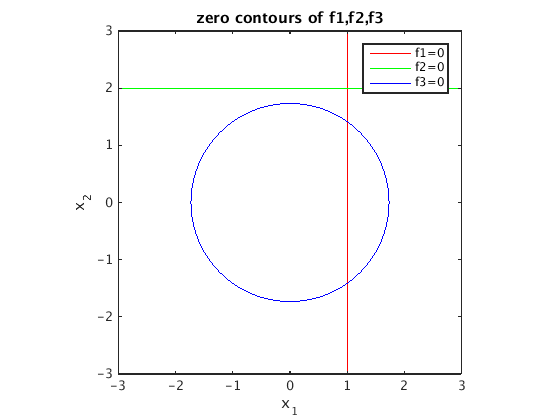
Perform 10 Gauss-Newton steps starting with [0;0]

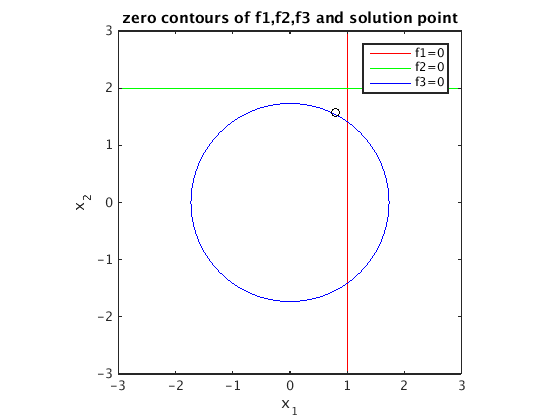
x = [0;0];           % initial guess
for i=1:10
  b = f(x);          % evaluate f
  fprintf('x=[%20.17g,%20.17g], ||f(x)||=%20.17g\n',x,norm(b))
  A = fp(x);         % evaluate Jacobian
  d = -A\b;          % solve norm(A*d+b)=min
  x = x + d;
end

plot(x(1),x(2),'ko'); hold off %    mark solution point with 'o'
title('zero contours of f1,f2,f3 and solution point')

x=[                   0,                   0], ||f(x)||=  3.7416573867739409
x=[                   1,                   2], ||f(x)||=                   2
x=[ 0.80952380952380942,  1.6190476190476191], ||f(x)||= 0.50787576572339488
x=[ 0.79127532704128101,  1.5825506540825622], ||f(x)||= 0.48464618206378557
x=[ 0.79142841595063729,  1.5828568319012746], ||f(x)||= 0.48464457916624887
x=[ 0.79142541916499731,  1.5828508383299948], ||f(x)||=  0.4846445785517931
x=[ 0.79142547754473658,  1.5828509550894729], ||f(x)||=  0.4846445785515599
x=[ 0.79142547640734506,  1.5828509528146903], ||f(x)||= 0.48464457855155979
x=[ 0.79142547642950456,  1.5828509528590089], ||f(x)||=  0.4846445785515599
x=[ 0.79142547642907268,  1.5828509528581454], ||f(x)||= 0.48464457855155973

Find errors

We see that we have convergence of order 1: the error gets multiplied by about .02 with each iteration.

xs = x;              % xs is exact solution which we just found
x = [0;0];           % initial guess
olderr = NaN;
for i=1:10
  b = f(x);          % evaluate f
  A = fp(x);         % evaluate Jacobian
  d = -A\b;          % solve norm(A*d+b)=min
  x = x + d;
  err = norm(x-xs);
  fprintf('||x-xs||=%8.2e, ratio=%g\n',err,err/olderr)
  olderr = err;
end

||x-xs||=4.66e-01, ratio=NaN
||x-xs||=4.05e-02, ratio=0.0867715
||x-xs||=3.36e-04, ratio=0.00829631
||x-xs||=6.57e-06, ratio=0.0195773
||x-xs||=1.28e-07, ratio=0.0194807
||x-xs||=2.49e-09, ratio=0.0194826
||x-xs||=4.86e-11, ratio=0.0194828
||x-xs||=9.46e-13, ratio=0.0194728
||x-xs||=1.91e-14, ratio=0.0201451
||x-xs||=0.00e+00, ratio=0

Published with MATLAB® R2014b