Mathematics Department Sample Placement Exam

Note: This is a SAMPLE exam



Instructions
1. $ 25.01+36.5+200.35=$
  (a) $ 81.545$  
  (b) $ 228.91$
  (c) $ 229.01$
  (d) $ 261.41$
  (e) $ 261.86$
2. If $ 5$ is subtracted from $ 2.8$ then the result is
  (a) $ -2.3$  
  (b) $ -2.2$
  (c) $ 2.2$
  (d) $ 2.3$
  (e) $ 3.8$
3. $ -5\left[4-(-3)(2)\right]=$
  (a) $ -70$  
  (b) $ -50$
  (c) $ -10$
  (d) $ 5$
  (e) $ 10$
4. If $ \frac43x-\frac12=0$, then $ x=$
  (a) $ \frac38$  
  (b) $ \frac23$
  (c) $ \frac32$
  (d) $ \frac{11}6$
  (e) $ \frac83$
5. $ 8\frac14-5\frac23=$
  (a) $ 4$  
  (b) $ 3\frac7{12}$
  (c) $ 3\frac5{12}$
  (d) $ 2\frac7{12}$
  (e) $ 2$
6. $ (-8p^2q)(-4p^4q^5)=$
  (a) $ 32p^5q^6$  
  (b) $ 4p^{-4}q^{-2}$
  (c) $ 32p^6q^6$
  (d) $ 4p^5q^8$
  (e) $ -32p^5q^8$
7. If $ x^2+2x=3$, then $ x$ could equal
  (a) $ -3$  
  (b) $ -2$
  (c) $ -1$
  (d) 0
  (e) $ 3$
8. A theater has $ n$ rows of seats and the number of seats in each row is $ 4$ less than the number of rows. Which of the following represents the total number of seats in the theater?
  (a) $ n(n-4)$  
  (b) $ n+(n-4)$
  (c) $ n^2+4$
  (d) $ n(4-n)$
  (e) $ n^2-4$
9. Eggs are to be packed in cartons, each holding $ 12$ eggs. If there are $ 128$ eggs and as many cartons are filled as possible, how many eggs are left over?
  (a) $ 6$  
  (b) $ 8$
  (c) $ 10.667$
  (d) $ 10.7$
  (e) $ 1536$
10. The polynomial equation $ x(x^2+4)(x^2-x-6)=0$ has how many real roots?
  (a) One only  
  (b) Two only
  (c) Three only
  (d) Four only
  (e) Five
11. $ (7rs^5)(-3r^3s^4)=$
  (a) $ 4r^{-2}s$  
  (b) $ 21r^3s^9$
  (c) $ -21r^4s^9$
  (d) $ 4r^3s^{20}$
  (e) $ -21r^3s^{20}$
12. $ \frac{12k^2h-3kh^2}{3kh}$
  (a) $ 12k^2h-h$  
  (b) $ 4k-h$
  (c) $ 3$
  (d) $ 3kh$
  (e) $ 4k-3kh^2$
13. If $ 0.05x=20$ then $ x=$
  (a) $ 400$  
  (b) $ 100$
  (c) $ 19.95$
  (d) $ 4$
  (e) $ 1.00$
14. $ \sqrt{50p^{16}q^8}=$
  (a) $ 25p^8q^4$  
  (b) $ 5p^8q^4\sqrt2$
  (c) $ 25p^{16}q^8$
  (d) $ 5p^8q^4$
  (e) $ 5p^{14}q^6\sqrt2$
15. If $ f(a)=2a-1$ and $ g(a)=a^2$, then $ g(f(a))=$
  (a) $ a^2-2a+1$  
  (b) $ 2a^2+1$
  (c) $ 4a^2+1$
  (d) $ (2a-1)^2$
  (e) $ a^2(2a-1)$
16. $ 5x+7(x-5)-3(y-5)=$
  (a) $ 7x-3y$  
  (b) $ 7x-3y-20$
  (c) $ 12x-3y-10$
  (d) $ 12x-3y-50$
  (e) $ 12x-3y-20$
17. If $ 7^x=3$ then $ x=$
  (a) $ \frac37$  
  (b) $ \frac73$
  (c) $ \log_3(7)$
  (d) $ \log_7(3)$
  (e) $ \log_{10}(\frac73)$
18. If $ t=e^{x+2}$ then $ x=$
  (a) $ 2+\ln t$  
  (b) $ \frac{t+2}e$
  (c) $ \frac t e$
  (d) $ \ln(t-2)$
  (e) $ \ln t-2$
19. $ \frac{x^2-4}{5x}\cdot\frac{30}{3x-6}=$
  (a) $ 4$  
  (b) $ 2(x+2)$
  (c) $ \frac{2(x-2)}{x}$
  (d) $ \frac{2(x+2)}{x}$
  (e) $ \frac43$
20. The inequality $ x^2-14x>15$ is equivalent to
  (a) $ -3<x<5$  
  (b) $ -1<x<15$
  (c) $ 3<x<5$
  (d) $ x<-1$ or $ x>15$
  (e) $ x<3$ or $ x>5$
21. The inequality $ 4x-5<3x+7$ is equivalent to
  (a) $ x<48$  
  (b) $ x<12$
  (c) $ x<3$
  (d) $ x<\frac54$
  (e) $ x<-2$
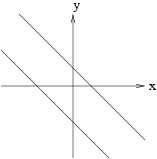
22. The two parallel lines represent the graph of which of the following two pairs of equations?
  (a) $ x-2y=3$ and $ x-2y=7$
  (b) $ x+y=1$ and $ x+y=-2$
  (c) $ x+y=3$ and $ 2x+2y=6$
  (d) $ x+y=3$ and $ x-y=5$
  (e) $ x-y=7$ and $ x-y=14$
23. In the system of equations

\begin{equation*}\left\{ \begin{aligned} x+2y & = 5 \\ 4x-6y & = 9 \end{aligned}\right\}\end{equation*}
  (a) $ x=0$  
  (b) $ x=\frac{11}{14}$
  (c) $ x=2$
  (d) $ x=\frac{24}7$
  (e) $ x=5$
24. If $ f(x)=x^2-kx-3$ and $ f(2)=9$, then $ k=$
  (a) $ -5$  
  (b) $ -4$
  (c) $ 2$
  (d) $ 4$
  (e) $ 9$
25. $ \left(8\right)^{2/3}\left(16\right)^{1/4}=$
  (a) $ 2$  
  (b) $ 4$
  (c) $ 8$
  (d) $ 16$
  (e) $ 32$
26. If $ \log_{10}s=4$ then $ s=$
  (a) $ \frac1{10,000}$  
  (b) $ \frac4{10}$
  (c) $ 10$
  (d) $ 1,000$
  (e) $ 10,000$
27. Of the following numbers, which is largest?
  (a) $ \cos(0)$  
  (b) $ \cos(\frac{\pi}6)$
  (c) $ \cos(\frac{\pi}4)$
  (d) $ \cos(\frac{\pi}3)$
  (e) $ \cos(\pi)$
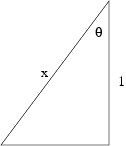
28. In the right triangle shown, $ \tan\theta=$
  (a) $ x$
  (b) $ x\sqrt{x^2-1}$
  (c) $ x^2+1$
  (d) $ \frac12(x^2-1)$
  (e) $ \sqrt{x^2-1}$
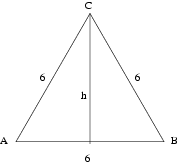
29. Triangle $ ABC$ is an equilateral triangle. The height $ h$ is :
  (a) $ 3$
  (b) $ 3\sqrt3$
  (c) $ 6\sqrt3$
  (d) $ 3\sqrt2$
  (e) $ 6\sqrt2$
30. When $ \frac{\pi}2<\theta<\frac{3\pi}4$, which of the following could possibly be $ \tan\theta?$
  (a) $ -8$  
  (b) $ -\frac18$
  (c) 0
  (d) $ \frac18$
  (e) $ 8$
31. For all real numbers $ x$, $ \cos^2(x)-\sin^2(x)=$
  (a) 0  
  (b) $ 1$
  (c) $ \sin(2x)$
  (d) $ \cos(2x)$
  (e) $ \cos(\frac{x}2)$
32. If $ f$ is a function whose graph is the parabola shown, then $ f(x)<0$ whenever
  (a) $ x>0$
  (b) $ x>-3$
  (c) $ x<2$
  (d) $ x<-3$ or $ x>2$
  (e) $ -3<x<2$

Please choose from the following grading options:

Will give you simply a count of correct vs. incorrect.
Will flag only the incorrect problems (so you can try again).
Will flag both the incorrect problems and the answers.
Retry the test from the beginning.