clear all

syms x y;
ezsurf(sqrt(x^2+y^2))
view([10,10,10])

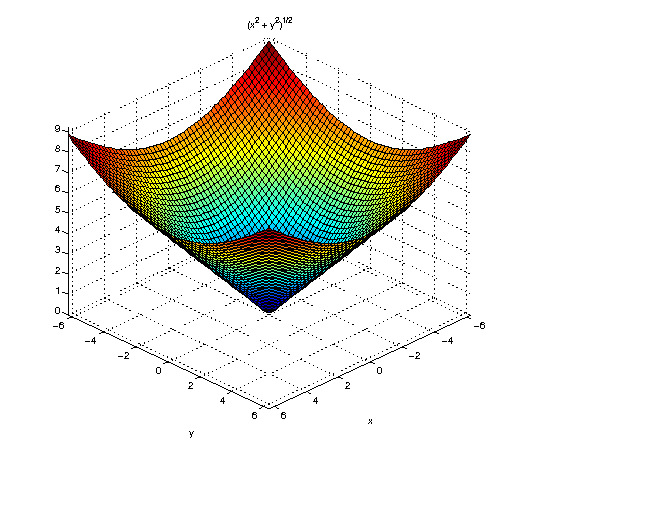
ezsurf(sqrt(9-x^2-y^2))
view([10,10,10])

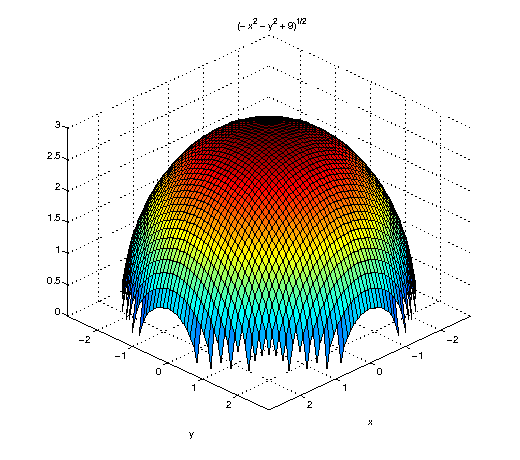
[xbunch,zbunch]=meshgrid(-5:0.1:5,-5:0.1:5);
f=4-x^2;
surf(xbunch,subs(f,{x,y},{xbunch,zbunch}),zbunch)
view([10 10 10])

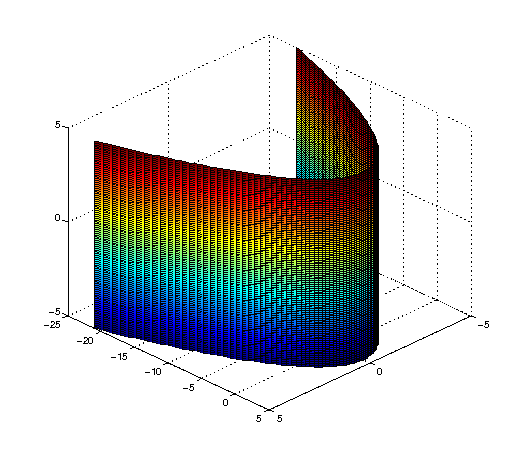
diff(x*sin(x^2*y),x)

 
ans =
 
sin(x^2*y) + 2*x^2*y*cos(x^2*y)
 

diff(diff((x^2-y)/(x+y),y),x)

 
ans =
 
1/(x + y)^2 - (2*x)/(x + y)^2 - (2*(y - x^2))/(x + y)^3
 

jacobian(x*log(x*y^2)+x*y,[x y])

 
ans =
 
[ y + log(x*y^2) + 1, x + (2*x)/y]
 

subs(jacobian(5*x^3*y^2-y/x,[x y]),{x,y},{-1,0})

ans =

     0     1

a=[2 -3];
dot((a/norm(a)),subs(jacobian(x^2+y^3,[x y]),{x,y},{2,-2}))

ans =

   -7.7658

f=(y-2)*log(x*y);
[xsoln,ysoln]=solve(jacobian(f,[x y]))

 
xsoln =
 
1/2
 
 
ysoln =
 
2
 

So the solution above is just (1/2,2).

f=x^3+y^3-6*x*y;
[xsoln,ysoln]=solve(jacobian(f,[x y]))

 
xsoln =
 
               0
               2
   3^(1/2)*i - 1
 - 3^(1/2)*i - 1
 
 
ysoln =
 
               0
               2
 - 3^(1/2)*i - 1
   3^(1/2)*i - 1
 

So the solutions above are (0,0) and (2,2). Ignore the complex.

clear all;
syms x y L;
f=x*y^2;
g=x^2+y^2-16;
firstpart=jacobian(f,[x y])-L*jacobian(g,[x y]);
[Lsoln,xsoln,ysoln]=solve(firstpart,g)
subs(f,{x,y},{xsoln,ysoln})

 
Lsoln =
 
              0
              0
  (4*3^(1/2))/3
  (4*3^(1/2))/3
 -(4*3^(1/2))/3
 -(4*3^(1/2))/3
 
 
xsoln =
 
              4
             -4
  (4*3^(1/2))/3
  (4*3^(1/2))/3
 -(4*3^(1/2))/3
 -(4*3^(1/2))/3
 
 
ysoln =
 
              0
              0
  (4*6^(1/2))/3
 -(4*6^(1/2))/3
  (4*6^(1/2))/3
 -(4*6^(1/2))/3
 
 
ans =
 
                0
                0
  (128*3^(1/2))/9
  (128*3^(1/2))/9
 -(128*3^(1/2))/9
 -(128*3^(1/2))/9
 

So the maximum is (128*3^(1/2))/9 at (4*3^(1/2)/3,+/-(4*6^(1/2))/3) and the minimum is -(128*3^(1/2))/9 at (-4*3^(1/2)/3,+/-(4*6^(1/2))/3).

Published with MATLAB® 7.9