MATH/CMSC 206 - Introduction to Matlab

Solving a Differential Equation

Introduction
Initial Value Problems
Plotting a solution.
Compound Example
An Example with Variables
Self-Test

Introduction

Matlab is quite powerful when it comes to solving differential equations. The standard command is dsolve (think Differential Solve) and has the format dsolve('equation','variable'). Here equation is a differential equation in the form of a string and variable is the independent variable. For example suppose we wished to solve dy/dx=2*y.

We type this into Matlab as:

dsolve('Dy=2*y','x')

 
ans =
 
C14*exp(2*x)

Note that Dy represents the derivative of the variable y. Also we should note here that you may get a differently numbered constant C1, C2, etc. depending upon how many constants that have shown up in Matlab for you. Don't worry for now about how they're numbered. We can use higher derivatives like D2y and D3y. For example if we type:

dsolve('D2y=2*y','x')

 
ans =
 
C16*exp(2^(1/2)*x) + C17/exp(2^(1/2)*x)

Initial Value Problems

We can also state initial conditions using the form dsolve('equation','initial condition','variable') where initial condition is also a string. For example:

dsolve('Dy=2*y','y(0)=5','x')

 
ans =
 
5*exp(2*x)

Matlab can of course do much more with differential equations as we'll see but for now just appreciate that it can handle most straightfoward examples with no problem at all.

Plotting a solution.

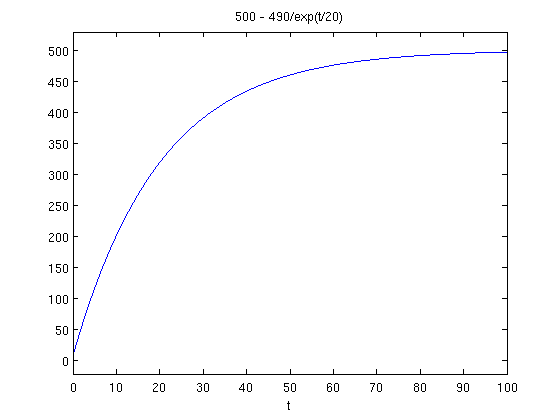
Plotting a solution is as easy as wrapping dsolve in ezplot:

ezplot(dsolve('Dy=0.05*(500-y)','y(0)=10','t'),[0,100])

Compound Example

Here's an example of a single Matlab line which will solve the initial value problem y'+3y+10=0 with y(1)=2, set the result equal to 0 and solve for x.

solve(dsolve('Dy+3*y+10=0','y(1)=2','x'),'x')

 
ans =
 
1 - log(5/8)/3

You can also set the result to a nonzero value with this totally confusing command:

solve(strcat(char(dsolve('Dy+3*y+10=0','y(1)=2','x'),'x'),'=20000'))

 
ans =
 
1 - log(30005/8)/3

An Example with Variables

You may notice the the following:

a=2;b=3;
dsolve('Dy=a*x+b','x')

 
ans =
 
(a*x^2)/2 + b*x + C25

This is annoying. You wanted a and b to be in the answer! The point is that 'Dy=a*x+b' is treated as a string and therefore a and b as just letters. They're not given their values. To get around this you can use different variables in the differential equation and then substitute in a and b:

a=2;b=3;
syms m n;
subs(dsolve('Dy=m*x+n','x'),{m,n},{a,b})

 
ans =
 
x^2 + 3*x + C27

Pay close attention to what this does. We solve using m and n as variables and then in place of m and n we substitute a and b. In this case the values are plugged in. Notice that the {m,n},{a,b} notation puts a=2 in place of m and b=3 in place of n.

Self-Test

Use Matlab to find the generic form of the function whose derivative is 15 percent of the original function.
Use Matlab to solve the separable differential equation dy/dt=y+y*sqrt(t).
Find a function passing through (0,2) and whose derivative satisfies y'-2y+x=5.
In a single command entry perform the answer to number 3 and also plug x=1 into the result.

Answers to Self-Test