| KEY IN |
DISPLAY |
EXPLANATION |
| PRGM -> -> ENTER SIMPSON | Prgm 1: SIMPSON | Program named "SIMPSON" |
| 2nd VARS 5 2 | FnOff | Deselects all functions |
Disp 2nd  "LOWERLIMIT" "LOWERLIMIT" | Disp "LOWERLIMIT" | Lower limit of integration |
Input  A A | Input A | After ?, type in the lower limit of integration |
Disp 2nd  "UPPERLIMIT" "UPPERLIMIT" | Disp "UPPERLIMIT" | Upper limit of integration |
Input  B B | Input B | After ?, type in the upper limit of integration |
Disp 2nd  "N "N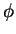 SUBINTERVALS" SUBINTERVALS" | Disp "N SUBINTERVALS" | Number of subintervals for [A, B] is N |
Disp 2nd  "ENTER EVEN N" "ENTER EVEN N" | Disp "ENTER EVEN N" | The even integer N is to be entered |
Input  N N | Input N | After ?, type in N |
0 STO  S S | 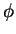 -> S -> S | 0 is stored in location S (for Simpson's Rule) |
0 STO  V V | 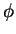 -> V -> V | 0 is stored in location V (for the Trapezoidal Rule) |
( B - B -  A) A)
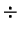 (
( N) STO N) STO  W W | (B - A)/N -> W | Subinterval width (B-A)/N stored in location W |
1 STO  J J | 1 -> J | 1 is stored in location J |
| Lbl 1 | Lbl 1 | Start of loop |
 A + 2( A + 2( J - 1) J - 1) W STO W STO  L L | A + 2(J - 1)W -> L | Left endpoint of [A+2(j-1)W, A+2jW] stored in L |
 A + 2 A + 2 J J W STO W STO  R R | A + 2JW -> R | Right endpoint of [A+2(j-1)W, A+2jW] stored in R |
( L + L +  R) R) 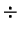 2 STO 2 STO  M M | (L + R)/2 -> M | Midpoint of [A+2(j-1)W, A+2jW] stored in M |
 L STO X,T, L STO X,T,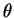 | L -> X | L is stored in location X |
2nd VARS 1 1 STO  L L | Y1 -> L | Y1(L) is stored in location L |
 M STO X,T, M STO X,T,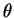 | M -> X | M is stored in location X |
2nd VARS 1 1 STO  M M | Y1 -> M | Y1(M) is stored in location M |
 R STO X,T, R STO X,T,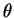 | R -> X | R is stored in location X |
2nd VARS 1 1 STO  R R | Y1 ->
R | Y1(R) is stored in location R |
 W( W( L+4 L+4 M+ M+ R) R)
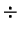 3 +
3 +  S STO S STO
 S S | W(L+4M+R)/3 + S
-> S | New sum is stored in location S (for Simp. Rule) |
 W( W( L+2 L+2 M+ M+ R) R)
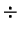 2 +
2 +  V STO V STO  V V | W(L+2M+R)/2 +V -> V | New sum is stored in location V (for Trap. Rule) |
IS >  J , J ,  N/2) N/2) | IS > (J,N/2) | Increment J one step. If J>N/2, skip next command |
| Goto 1 | Goto 1 | Program returns to Lbl 1 and loops again |
Disp 2nd  "Simpson Rule" "Simpson Rule" | Disp. "Simpson Rule" | Prepares for the Simpson's Rule approximation |
Disp  S S | Disp S | Displays the Simpson's Rule approximation S |
Disp 2nd  "Trap. Rule" "Trap. Rule" | Disp. "Trap. Rule" | Prepares for the Trapezoidal Rule approximation |
Disp  V V | Disp V | Displays the Trapezoidal Rule approximation V |
 "LOWERLIMIT"
"LOWERLIMIT" A
A "UPPERLIMIT"
"UPPERLIMIT" B
B "N
"N SUBINTERVALS"
SUBINTERVALS"  "ENTER EVEN N"
"ENTER EVEN N" N
N  S
S -> S
-> S V
V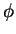 -> V
-> V B -
B -  A)
A)
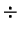 (
( N) STO
N) STO  W
W J
J A + 2(
A + 2( J - 1)
J - 1) W STO
W STO  L
L A + 2
A + 2 J
J W STO
W STO  R
R L +
L +  R)
R) 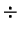 2 STO
2 STO  M
M L STO X,T,
L STO X,T,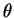
 L
L M STO X,T,
M STO X,T,
 M
M R STO X,T,
R STO X,T,
 R
R W(
W( L+4
L+4 M+
M+ R)
R)
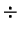 3 +
3 +  S STO
S STO
 S
S W(
W( L+2
L+2 M+
M+ R)
R)
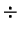 2 +
2 +  V STO
V STO  V
V  J ,
J ,  N/2)
N/2) "Simpson Rule"
"Simpson Rule" S
S "Trap. Rule"
"Trap. Rule" V
V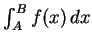 do the
following:
do the
following: