MATH 241 Final Exam from Spring 1997

Note: This exam was originally written when we were using Mathematica in the course. All the Mathematica code has been translated into MATLAB.

(30 points) You are given the points P=(0,1,3), Q=(2,1,1), and R=(-1,3,-2). Find:
1. An equation for the plane containing the points P, Q, and R.
2. A unit vector perpendicular to this plane.
3. The area of the triangle PQR.
4. The distance from the origin to the plane containing the points P, Q, and R.

(25 points) Answer this question with the help of the MATLAB code that follows. Consider the curve parametrized by r(t) = ((2t+1) / (t-1))i + (t² / (t-1))j + (t+2)k.
1. Determine the curvature and torsion of the curve at the point r(½).
2. Determine the Frenet vectors T, N, and B at r(½).
3. What geometric quantity provides a measure of non-planarity for curves? Is the curve parametrized by r(t) planar?
MATLAB code for Problem 2
```
>> syms t
>> r = [(2*t+1)/(t-1), t^2/(t-1), t+2];
>> v=diff(r); a=diff(v); g=diff(a); h=cross(v,a);
>> simplify(h*transpose(g))
 
ans =
 
0
 
>> subs(v, t, 1/2)

ans =

   -12    -3     1

>> subs(h, t, 1/2)

ans =

    16   -48    48

>> subs(cross(h,v), t, 1/2)

ans =

    96  -592  -624
```

(25 points) Let g(x, y, z) be a function of 3 variables defined by g(x, y, z) = 2x² + y² + 3z²/2, and let S be the level surface defined by g(x, y, z) = 9.
1. Find an equation for the tangent plane to S at the point (1,1,2).
2. Compute the derivative with respect to t of g(t, t, 2t) at t = 1.

(25 points) Answer this problem on the basis of the MATLAB code that follows. Identify all critical points of the function f(x, y) = x³ + y³ - xy² + 2yx² - x² - y² and identify each one as a local maximum, local minimum, saddle point, or degenerate critical point. Locate all critical points on the plot and explain how the shapes of the contours are consistent with your results.

MATLAB code for Problem 4

>> syms x y
>> f=x^3+y^3-x*y^2+2*x^2*y-x^2-y^2; pretty(f)
 
                        3    3      2      2      2    2
                       x  + y  - x y  + 2 x  y - x  - y
>> fx=diff(f,x); fy=diff(f,y); fxx=diff(fx,x); fyy=diff(fy,y);
>> fxy=diff(fx,y); disc=fxx*fyy-fxy^2;
>> [xcr,ycr]=solve(fx,fy);
>> discf=inline(vectorize(disc)); fxxf=inline(vectorize(fxx));
>> double([xcr,ycr,discf(xcr,ycr),fxxf(xcr,ycr)])

ans =

         0         0    4.0000   -2.0000
   -0.2222    0.4444   -4.8889   -1.5556
    0.3022    0.7912    6.2413    2.9780
    0.4564    0.1743   -4.8620    1.4358

>> ff=inline(vectorize(f));
>> [xx,yy]=meshgrid(-.5:.01:.5, -.2:.01:.8); zz=ff(xx,yy);
>> contour(xx,yy,zz,-2.5:.05:2.5)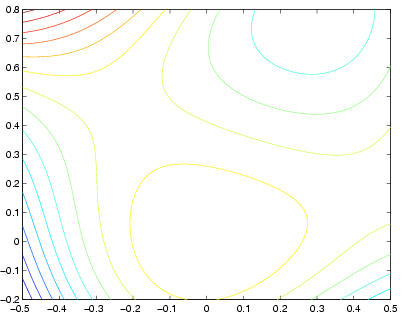

(50 points) The MATLAB code that follows computes three integrals numerically. For each one, sketch the region of integration and obtain a precise value for the integral. In order to do this, you will need to reformulate each integral in some way. The numerical values obtained by MATLAB, which are only approximate, can be used to check your answers.
MATLAB code for Problem 5
```
>> syms x y z
>> addpath nit
>> numint3(z,z,sqrt(x^2+y^2),2,y,-sqrt(4-x^2),sqrt(4-x^2),x,-2,2)

ans =

   12.5657

>> newnumint2(sin(12*x-x^3),x,0,sqrt(y/3),y,0,12)

ans =

    1.9577

>> newnumint2(x^2,y,0,3*sqrt(1-x^2/4),x,0,2)

ans =

    4.7128
```

(20 points) Answer this question with the help of the following MATLAB code.

MATLAB code for Problem 6


>> syms x y z
>> curl=inline(['[diff(F3,y)-diff(F2,z),', ...
'diff(F1,z)-diff(F3,x), diff(F2,x)-diff(F1,y)]'], 'F1','F2','F3','x','y','z')

curl =

     Inline function:
     curl(F1,F2,F3,x,y,z) = [diff(F3,y)-diff(F2,z),diff(F1,z)-diff(F3,x), 
     diff(F2,x)-diff(F1,y)]
>> grad = inline('[diff(f,x),diff(f,y),diff(f,z)]', 'f', 'x','y','z')

grad =

     Inline function:
     grad(f,x,y,z) = [diff(f,x),diff(f,y),diff(f,z)]
>> curl(x,y,z,x,y,z)
 
ans =
 
[ 0, 0, 0]
 
>> term1=curl('f(x,y,z)*F1(x,y,z)','f(x,y,z)*F2(x,y,z)','f(x,y,z)*F3(x,y,z)',...
x,y,z)
 
term1 =
 
[ 
diff(f(x,y,z),y)*F3(x,y,z)+f(x,y,z)*diff(F3(x,y,z),y)-diff(f(x,y,z),z)*F2(x,y,z)
-f(x,y,z)*diff(F2(x,y,z),z), 
diff(f(x,y,z),z)*F1(x,y,z)+f(x,y,z)*diff(F1(x,y,z),z)-diff(f(x,y,z),x)*F3(x,y,z)
-f(x,y,z)*diff(F3(x,y,z),x), 
diff(f(x,y,z),x)*F2(x,y,z)+f(x,y,z)*diff(F2(x,y,z),x)-diff(f(x,y,z),y)*F1(x,y,z)
-f(x,y,z)*diff(F1(x,y,z),y)]
 
>> term2='f(x,y,z)'*curl('F1(x,y,z)','F2(x,y,z)','F3(x,y,z)',x,y,z)
 
term2 =
 
[ f(x,y,z)*(diff(F3(x,y,z),y)-diff(F2(x,y,z),z)), 
f(x,y,z)*(diff(F1(x,y,z),z)-diff(F3(x,y,z),x)), 
f(x,y,z)*(diff(F2(x,y,z),x)-diff(F1(x,y,z),y))]
 
>> term3=cross(sym(grad('f(x,y,z)',x,y,z)), ...
sym('[F1(x,y,z),F2(x,y,z),F3(x,y,z)]'))
 
term3 =
 
[ diff(f(x,y,z),y)*F3(x,y,z)-diff(f(x,y,z),z)*F2(x,y,z), 
diff(f(x,y,z),z)*F1(x,y,z)-diff(f(x,y,z),x)*F3(x,y,z), 
diff(f(x,y,z),x)*F2(x,y,z)-diff(f(x,y,z),y)*F1(x,y,z)]
 
>> simplify(term1-term2-term3)
 
ans =
 
[ 0, 0, 0]

What simple identities about the curl and gradient are being proved in this MATLAB session? (State the result in standard mathematical notation, not MATLAB notation.)
Use the identities to compute the curl of F = [(x³ + y³ + z³) / 3] · (xi + yj + zk).

(25 points) The diagram below, generated in MATLAB, shows four vector fields F, each accompanied by an oriented curve C. Answer the following questions about them, assuming, if necessary, that the vector fields are extended in three dimensions to be constant in the z-direction.
MATLAB pictures for Problem 7
1. One of the vector fields has zero divergence. Which one is it and why?
2. Two of the vector fields have zero curl. Which ones are they and why?
3. Three of the line integrals of F·dr along C are zero. Which ones are they and why?
4. Explain how your answers in the other 3 parts are consistent.

MATH 241 Final Exam from Spring 1997

MATLAB code for Problem 2

MATLAB code for Problem 4

MATLAB code for Problem 5

MATLAB code for Problem 6

MATLAB pictures for Problem 7