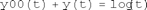
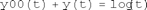
dsolve('D2y - y = log(t)')
ans = exp(-t)*C2+exp(t)*C1-1/2*(2*exp(t)*log(t)+Ei(1,-t)+exp(2*t)*Ei(1,t))*exp(-t)
The answer involves a function Ei. What does that mean?
help Ei mhelp Ei
Ei.m not found.
Use the Help browser Search tab to <a href="matlab:docsearch Ei">search the documentation</a>, or
type "<a href="matlab:help help">help help</a>" for help command options, such as help for methods.
Ei - The Exponential Integral
Calling Sequence
Ei(x)
Ei(n, x)
Parameters
x - algebraic expression
n - algebraic expression, understood to be a non-negative integer
Description
- The exponential integrals, Ei(n,x), where n is a non-negative integer, are
defined for Re(x)>0 by
Ei(n,x) = int(exp(-x*t)/t^n, t=1..infinity)
and are extended by analytic continuation to the entire complex plane, with
the exception of the point 0 in the case of Ei(1, x). For all of these
functions, 0 is a branch point and the negative real axis is the branch cut.
The values on the branch cut are assigned in such a way that the functions are
continuous in the direction of increasing argument.
The exponential integrals are related to the incomplete Gamma function by
Ei(n,x) = x^(n-1) GAMMA(1-n,x)
- The 1-argument exponential integral is a Cauchy Principal Value integral,
defined only for real arguments x, as follows:
Ei(x) = PV-int(exp(t)/t, t=-infinity..x)
For x<0, Ei(x) = -Ei(1,-x).
- Reference: M. Abramowitz and I. Stegun, Handbook of Mathematical Functions,
Dover Publications Inc., New York, (1965).
Examples
> Ei(1,1.);
0.2193839344
> Ei(1,-1.);
-1.895117816 - 3.141592654 I
> expand(Ei(3,x));
2
1/2 exp(-x) - 1/2 x exp(-x) + 1/2 x Ei(1, x)
> simplify(Ei(1,I*x)+Ei(1,-I*x));
-2 Ci(x) - Pi I + Pi csgn(x) I
> Ei(5, 3+I);
Ei(5, 3 + I)
> evalf(%);
0.002746760454 - 0.006023680639 I
> Ei(1.);
1.895117816
> Ei(-1.);
-0.2193839344
> int(exp(-3*t)/t, t=-x..infinity, CauchyPrincipalValue);
-Ei(3 x)
See Also
Ci, Li, expand, convert, simplify, int, inifcns
It seems Ei is a maple function, not a matlab function. The corresponding matlab function is expint.
clear syms t v1 v2 % Solutions of the homogeneous equation are exp(t) and exp(-t), so: y = 'v1(t)'*exp(t) + 'v2(t)'*exp(-t) diff(y, t)
y = v1(t)*exp(t)+v2(t)*exp(-t) ans = diff(v1(t),t)*exp(t)+v1(t)*exp(t)+diff(v2(t),t)*exp(-t)-v2(t)*exp(-t)
Note that there are four terms. We can get this down to two as long as we assume that two of them sum to zero.
y1 = subs(ans, diff('v2(t)',t)*exp(-t), -diff('v1(t)',t)*exp(t))
y1 = v1(t)*exp(t)-v2(t)*exp(-t)
Now we proceed to take the second derivative using the same assumptions.
y2 = diff(y1, t) y2 = subs(y2, diff('v2(t)',t)*exp(-t), -diff('v1(t)',t)*exp(t))
y2 = diff(v1(t),t)*exp(t)+v1(t)*exp(t)-diff(v2(t),t)*exp(-t)+v2(t)*exp(-t) y2 = 2*diff(v1(t),t)*exp(t)+v1(t)*exp(t)+v2(t)*exp(-t)
Now we need to set y2 - y equal to log(t).
y2-y
ans = 2*diff(v1(t),t)*exp(t)
So v1 is obtained by integrating log(t)*exp(-t)/2
v1 = int(log(t)*exp(-t)/2, t)
v1 = -1/2*exp(-t)*log(t)-1/2*Ei(1,t)
And since exp(t)*d(v1)/dt = - exp(-t)*d(v2)/dt, v2 is obtained by integrating - log(t)*exp(t)/2.
v2 = int(-log(t)*exp(t)/2, t)
v2 = -1/2*exp(t)*log(t)-1/2*Ei(1,-t)
y = subs(subs(y, 'v1(t)', v1), 'v2(t)', v2)
y = (-1/2*exp(-t)*log(t)-1/2*Ei(1,t))*exp(t)+(-1/2*exp(t)*log(t)-1/2*Ei(1,-t))*exp(-t)
Check:
simplify(diff(y, t, 2) - y)
ans = log(t)