Newton's Method of Solving Equations by Approximation
syms y p q r s f = y^3-2*y-5
f = y^3 - 2*y - 5
By inspection, we see f has only one real root and it's close to 2.
ezplot(f, [-2, 3]), grid
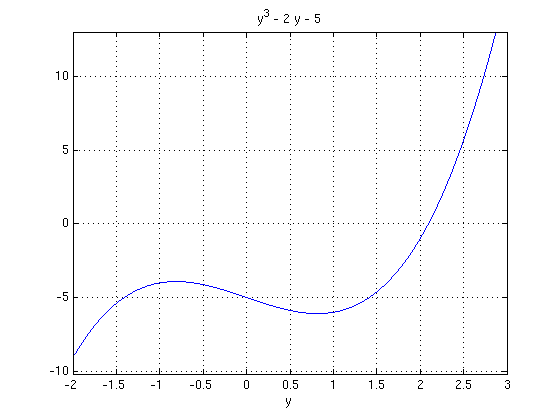
So write y = 2 + p and simplify.
f1 = simplify(expand(subs(f, y, 2+p)))
f1 = p^3 + 6*p^2 + 10*p - 1
Since p is small, its square and cube are even smaller. So through away higher order terms and set the linear terms equal to zero to get the next approximation.
v1 = solve(10*p - 1) f2 = simplify(expand(subs(f1, p, q + v1)))
v1 = 1/10 f2 = q^3 + (63*q^2)/10 + (1123*q)/100 + 61/1000
Again, since q is small, throw away the higher-order terms and set the linear terms to zero to get the next approximation.
v2 = solve((1123*q)/100 + 61/1000) f3 = simplify(expand(subs(f2, q, r + v2)))
v2 = -61/11230 f3 = r^3 + (35283*r^2)/5615 + (351906913*r)/31528225 + 32878756/177030983375
And again
v3 = solve((351906913*r)/31528225 + 32878756/177030983375) f4 = simplify(expand(subs(f3, r, s + v3)))
v3 = -216030631306836110157925/12983073523760345535601442816 f4 = s^3 + (458078144102851907878350096630303*s^2)/72899957835914340182402101411840 + (59316387663281542164614388705466343061735328767391211729234919403*s)/5314403852478088608713754821846215047613130170655163721292185600 + 674018880300187728391539440764019652606452350032354674647687152162914158219124062649101/387419816768673392824459786078789849707278374816065488459054047874902411726799715298919317504000
And again
h = vpa(f4) v4 = solve(11.161437728452366387787531821058*s + 0.0000000017397635617143490891963159090982);
h = s^3 + 6.283654445094597908650087035368*s^2 + 11.161437728452366387787531821058*s + 0.0000000017397635617143490891963159090982
So here are our successive approximations with the corresponding values of f:
[vpa(2), vpa(subs(f,y,2))] [vpa(2 + v1), vpa(subs(f,y,2+v1))] [vpa(2 + v1 + v2), vpa(subs(f,y,2+v1+v2))] [vpa(2 + v1 + v2 + v3), vpa(subs(f,y,2+v1+v2+v3))] [vpa(2 + v1 + v2 + v3 + v4), vpa(subs(f,y,2+v1+v2+v3+v4))]
ans = [ 2.0, -1.0] ans = [ 2.1, 0.061] ans = [ 2.0945681211041852181656277827248, 0.00018572317327274746038505419334199] ans = [ 2.0945514816981993028833623451227, 0.0000000017397635617143490891963159090982] ans = [ 2.0945514815423265914960648422916, 0.00000000000000000015266951276651424479033893041292]