Exam 3
Contents
- 1(a): R is given as vertically simple region. Rewrite R as horizontally simple region.
- 1(b): Compute integral using change of variables
- 2(a): Consider ball with cylindrical hole. Find the volume using spherical coordinates.
- 2(b) Find the volume using cylindrical coordinates.
- 3(a),(c): Find the surface area of a part of a cone.
- 3(b) Find a normal vector N for the point (2,0,1)
1(a): R is given as vertically simple region. Rewrite R as horizontally simple region.
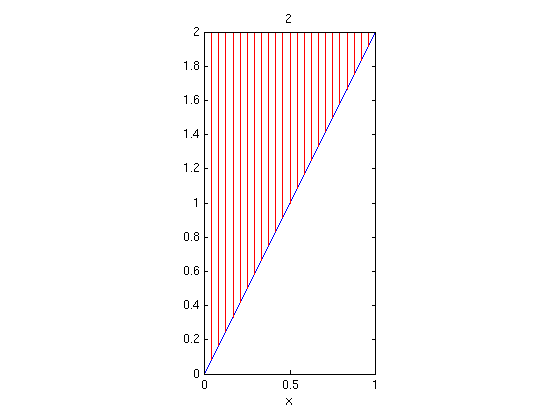
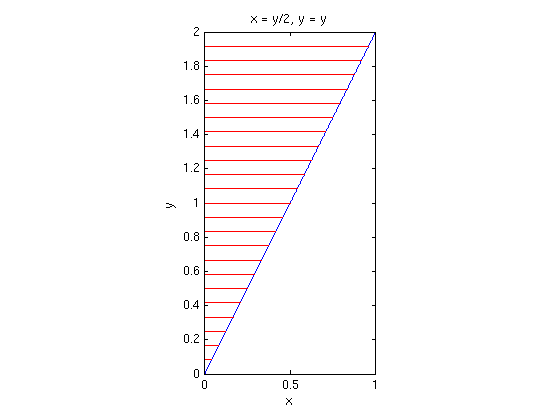
The region R consists of the points (x,y) with 0<=x<=1, 2*x<=y<=2.
Answer: The smallest y is 0 (for x=0), the largest y is 2, hence 0<=y<=2. For a given value y we must have 0<=x and 2*x<=y, hence 0<=x<=y/2.
syms x y real figure(1); regionvs(0,1,2*x,2) % plot vertically simple region axis equal; axis tight figure(2); regionhs(0,2,0,y/2) % plot horizontally simple region axis equal; axis tight
1(b): Compute integral using change of variables
Let f(x,y) = exp(x/y). Find the integral of f over the region R from (a), using the variables u=x/y and v=y.
Answer: We have r=(x,y)=(u*v,v). Since 0<=x<=y/2 we have 0<=x/y<=1/2 for u=x/y. We have 0<=v<=2 for v=y.
syms x y u v real r = [u*v,v]; % r=(x,y) in terms of u,v M = jacobian(r,[u v]) % Jacobian matrix of partial derivatives [x_u x_v; y_u, y_v] J = det(M) % Jacobian determinant (note J=v>=0) f = exp(x/y) fs = subs(f,{x,y},r) % write f in terms of u,v I = int(int(fs*J,v,0,2),u,0,1/2) % find integral using dx*dy = J*du*dv % Try to find integral using original x,y coordinates: I_orig = int(int(f,y,2*x,2),x,0,1) % gives same answer (but this is much harder to do by hand!)
M = [ v, u] [ 0, 1] J = v f = exp(x/y) fs = exp(u) I = 2*exp(1/2) - 2 I_orig = 2*exp(1/2) - 2
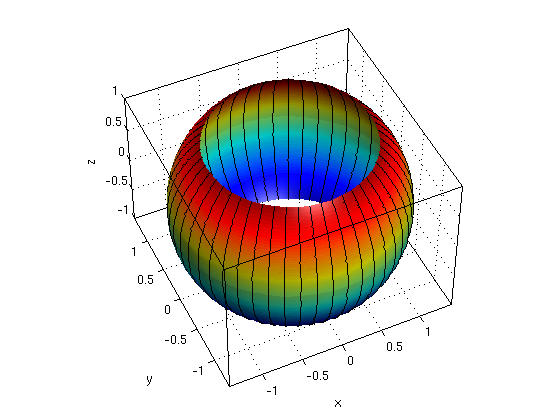
2(a): Consider ball with cylindrical hole. Find the volume using spherical coordinates.
The region D consists of the points (x,y,z) with x^2+y^2+z^2<=2 and x^2+y^2>=1.
Answer: We have on the boundary of the cylinder that r=1, with r=rho*sin(phi) this means rho=1/sin(phi). On the intersection of the sphere and cylinder we have rho=sqrt(2) and r=1, with r=rho*sin(phi) this means that 1 = sqrt(2)*sin(phi) or sin(phi)=1/sqrt(2) or phi=pi/4,3/4*pi.
Hence we have the limits 0<=theta<=2*pi, pi/4<=phi<=3/4*pi, 1/sin(phi)<=rho<=sqrt(2).
syms rho phi theta real Pi = sym('pi'); R = sym('sqrt(2)') a = 0; b = 2*Pi; % limits for theta g1 = Pi/4; g2 = 3/4*Pi; % limits for phi h1 = 1/sin(phi); h2 = R; % limits for rho ezsurfspher(h1,a,b,g1,g2); hold on % plot inner boundary ezsurfspher(h2,a,b,g1,g2); hold off % plot outer boundary nice3d; defaultlighting; view(-25,47) J = rho^2*sin(phi); % dV = J*drho*dphi*dtheta volume = int( int( int(J,rho,h1,h2), phi,g1,g2), theta,a,b)
R = 2^(1/2) volume = (4*pi)/3
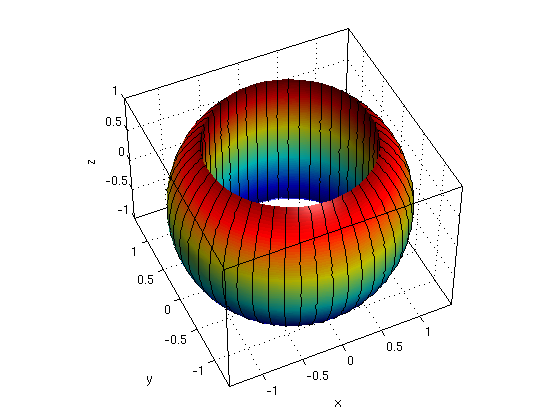
2(b) Find the volume using cylindrical coordinates.
We have limits 0<=theta<=2*pi, 1<=r<=sqrt(2), -sqrt(2-r^2)<=z<=sqrt(2-r^2)
syms r theta z real Pi = sym('pi'); R = sym('sqrt(2)') a = 0; b = 2*Pi; % limits for theta g1 = 1; g2 = R; % limits for r h1 = -sqrt(2-r^2); h2 = sqrt(2-r^2); % limits for z ezsurfpol(h1,a,b,g1,g2); hold on % plot lower boundary ezsurfpol(h2,a,b,g1,g2); hold off % plot upper boundary nice3d; defaultlighting; view(-25,47) J = r; % dV = J*dr*dtheta*dz volume = int( int( int(J,z,h1,h2), r,g1,g2), theta,a,b) % we get same value as in (a)!
R = 2^(1/2) volume = (4*pi)/3
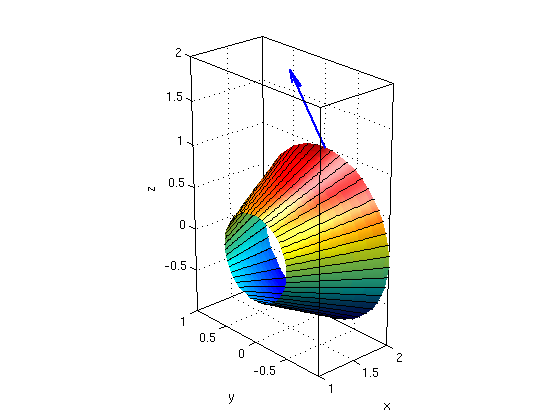
3(a),(c): Find the surface area of a part of a cone.
The surface consists of the points (x,y,z) with x/2=sqrt(y^2+z^2), z>=0, 1<=x<=2.
Answer: Let theta be the angle in the yz-plane. Then (x,y,z) = (x,x/2*cos(theta),x/2*sin(theta)) with the limits 0<=theta<=pi, 1<=z<=2.
syms x theta real r = [x, x/2*cos(theta), x/2*sin(theta)]; % parameterization rtheta = diff(r,theta) % w.r.t. theta rx = diff(r,x) % partial derivatives w.r.t x N = simplify( cross(rtheta,rx) ) % cross product normN = simplify(norm(N)) area = int( int(normN,x,1,2), theta,0,2*pi) ezsurfpar(r(1),r(2),r(3),0,2*pi,1,2) % plot the surface nice3d; view(-42,24); defaultlighting hold on
rtheta = [ 0, -(x*sin(theta))/2, (x*cos(theta))/2] rx = [ 1, cos(theta)/2, sin(theta)/2] N = [ -x/4, (x*cos(theta))/2, (x*sin(theta))/2] normN = (5^(1/2)*abs(x))/4 area = (3*pi*5^(1/2))/4
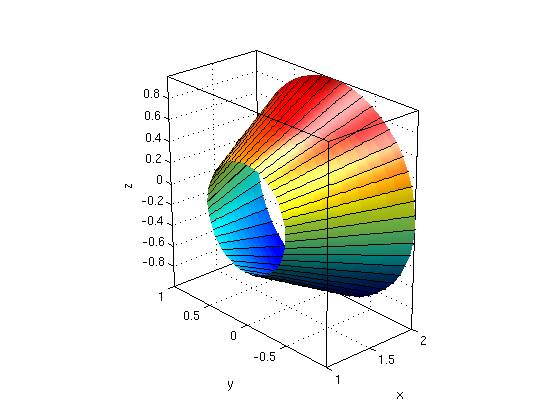
3(b) Find a normal vector N for the point (2,0,1)
Answer: We have (2,0,1) = (x,x/2*cos(theta),x/2*sin(theta)) for x=2, theta=pi/2
P = [2,0,1];
N0 = subs(N,{x,theta},{2,pi/2})
arrow3(P,N0); hold off; axis tight
N0 = [ -1/2, 0, 1]