Exam 4
Contents
- 1(a): Explain why flux over top boundary is zero.
- 1(b): Find the flux over the lateral boundary using r, theta.
- 1(c): Apply the divergence theorem and find the flux from (b) as a volume integral.
- 2(a): Find a work integral.
- 2(b): Find another work integral using the fundamental theorem of line integrals.
- 3(a): Find a line integral for a scalar function f
- 3(b): Find work integral using Green's theorem.
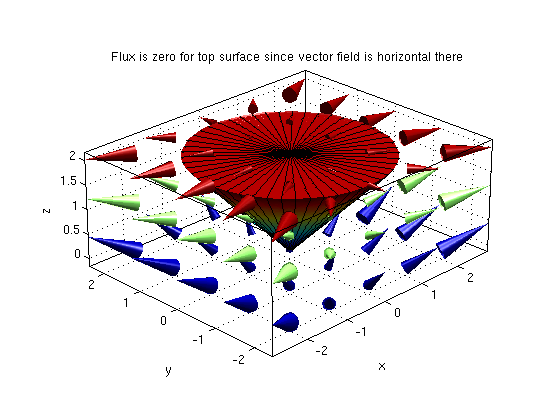
1(a): Explain why flux over top boundary is zero.
Consider cone with r<=z and 0<=z<=2. Let F=(2*x, y, 2-z).
Answer: For the top surface z=2 we have the normal vector n=(0,0,1). For z=2 we have F=(2*x,y,0). Hence the dot product of F and n is zero.
syms x y z r theta real ezsurfpol(r,0,2*pi,0,2); hold on % plot lateral boundary of D where z=r ezsurfpol(2,0,2*pi,0,2); % plot top boundary of D where z=2 nice3d F = [2*x, y, 2-z]; % given vector field F vectorfield3(F,-2:1:2,-2:1:2,0:1:2); hold off; view(-45,25) title('Flux is zero for top surface since vector field is horizontal there')
1(b): Find the flux over the lateral boundary using r, theta.
R = [r*cos(theta),r*sin(theta),r]; % parametrization R=(x,y,z) of lateral boundary of cone Rr = diff(R,r) Rtheta = diff(R,theta) N = simplify( cross(Rr,Rtheta) ) % N(3)=r>0, hence vector N points up % but vector n points down, hence need "-" below Fs = subs(F,{x,y,z},R) % substitute parametrization in F integrand = dot(Fs,N) flux = -int( int(integrand,r,0,2), theta,0,2*pi) % flux integral using r,theta % need "-" since N points in opposite direction of n
Rr = [ cos(theta), sin(theta), 1] Rtheta = [ -r*sin(theta), r*cos(theta), 0] N = [ -r*cos(theta), -r*sin(theta), r] Fs = [ 2*r*cos(theta), r*sin(theta), 2 - r] integrand = - 2*r^2*cos(theta)^2 - r^2*sin(theta)^2 - r*(r - 2) flux = (16*pi)/3
1(c): Apply the divergence theorem and find the flux from (b) as a volume integral.
We use cylindrical coordinates for the integral.
R = [r*cos(theta),r*sin(theta),z]; % cylindrical coordinates g = divergence(F,[x y z]) % find divergence of F gs = subs(g,{x,y,z},R) % substitute cylindrical coordinates in g flux = int( int( int(gs*r,z,r,2), r,0,2), theta,0,2*pi) % use dV = r*dr*dtheta*dz
g = 2 gs = 2 flux = (16*pi)/3
2(a): Find a work integral.
C is the straight line from (1,0,0) to (0,1,1), and the vector field is F=(x+y,y+z,z).
Answer: curl F = (-1,0,-1) is nonzero. Hence there is no potential f, and we cannot use the fundamental theorem of line integrals to find the work.
syms x y z t real P = [1,0,0]; Q = [0,1,1]; % endpoints of straight line C r = P + t*(Q-P) % parametrization r(t) of C, 0<=t<=1 rp = diff(r,t) % r'(t) F = [x+y, y+z, z]; % vector field F Fs = subs(F,{x,y,z},r) % substitute parametrization for x,y,z integrand = dot(Fs,rp) work = int(integrand,t,0,1) curlF = curl(F,[x y z]) % Note that curl is nonzero, hence there is no potential.
r = [ 1 - t, t, t] rp = [ -1, 1, 1] Fs = [ 1, 2*t, t] integrand = 3*t - 1 work = 1/2 curlF = -1 0 -1
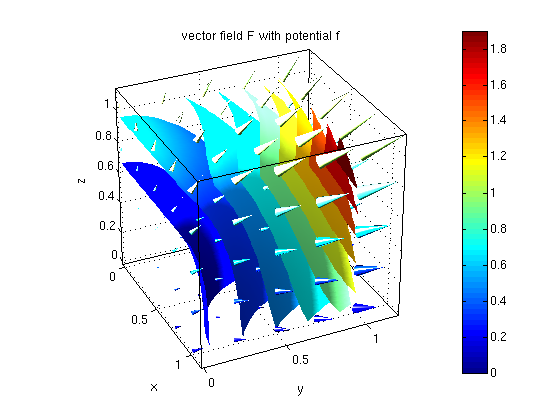
2(b): Find another work integral using the fundamental theorem of line integrals.
Now the vector field is F=(2*x*y, x^2+2*y*z, y^2+z^2).
F = [2*x*y, x^2+2*y*z, y^2+z^2]; f = potential(F,[x y z]) % find potential f work = subs(f,{x,y,z},Q) - subs(f,{x,y,z},P) % work is difference of potential at points Q and P vectorfield3(F,0:.25:1,0:.25:1,0:.25:1); hold on % plot vector field F ezisosurf(f,[0 1 0 1 0 1],.1:.2:2); colorbar; hold off % plot potential f nice3d; view(65,30); title('vector field F with potential f')
f = x^2*y + y^2*z + z^3/3 work = 4/3
3(a): Find a line integral for a scalar function f
Let C denote the circle x^2+y^2=9, with counterclockwise direction. Find the line integral of the function x^2+y over the curve C.
Answer: parametrization of circle: (x,y) = (3*cos(t),3*sin(t)), 0<=t<=2*pi
syms x y t real r = [3*cos(t),3*sin(t)]; % parametrization r(t) rp = diff(r,t) % r'(t) rpnorm = simplify( norm(rp) ) % ||r'|| f = x^2 + y; fs = subs(f,{x,y},r) % substitute parametrization in f integrand = fs*rpnorm I = int(integrand,t,0,2*pi) % line integral using ds = ||r'||*dt
rp = [ -3*sin(t), 3*cos(t)] rpnorm = 3 fs = 3*sin(t) + 9*cos(t)^2 integrand = 9*sin(t) + 27*cos(t)^2 I = 27*pi
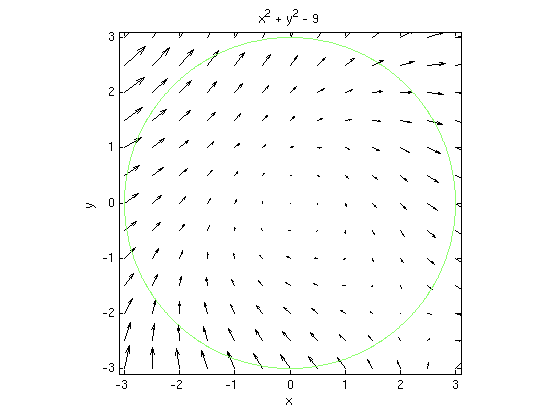
3(b): Find work integral using Green's theorem.
For the vector field F=[x^2+2*y, y^2-2*x] find the work over the curve C by using Green's theorem.
syms x y r theta real F = [x^2+2*y, y^2-2*x]; % vector field F G = diff(F(2),x) - diff(F(1),y) % find curl I = int( int( G*r, r,0,3), theta,0,2*pi) % integrate curl over circle using dA=r*dr*dtheta vectorfield(F,-3:.5:3,-3:.5:3); hold on % plot vector field ezplot(x^2+y^2-9,[-3 3 -3 3]); % plot circle hold off; axis([-3.1 3.1 -3.1 3.1])
G = -4 I = -36*pi