Examples Friday, Feb. 21

Contents

You need to download new m-files.

Download the files defaultlighting.m, surfcontour.m, ezcontourfill.m.

Function f(x,y) = x*y^2/(x^2+y^2) where we define f(0,0)=0.

This function is continuous for all x,y, as we showed in class.

syms x y real                 % define x,y as real symbolic values
f = x*y^2/(x^2+y^2);
ezsurf(f,[-1 1 -1 1])         % plot graph for x=-1...1, y=-1...1
surfcontour                   % add contours to surface (instead of grid)
defaultlighting               % illuminate with default lights
nice3d; view(-60,30)

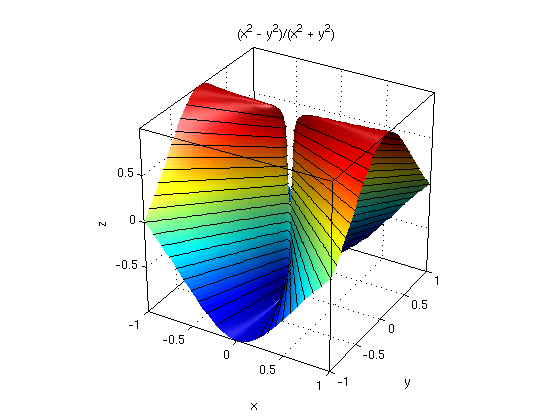
Function f(x,y) = (x^2-y^2)/(x^2+y^2)

This function is continuous for all (x,y) different from (0,0). In the point (0,0) the function does not have a limit. Note that on the x-axis we have f(x,0)=1, and on the y-axis we have f(0,y)=-1.

f = (x^2-y^2)/(x^2+y^2);
ezsurf(f,[-1 1 -1 1])         % plot graph for x=-1...1, y=-1...1
surfcontour                   % add contours to surface (instead of grid)
defaultlighting               % illuminate with default lights
nice3d; view(30,30)

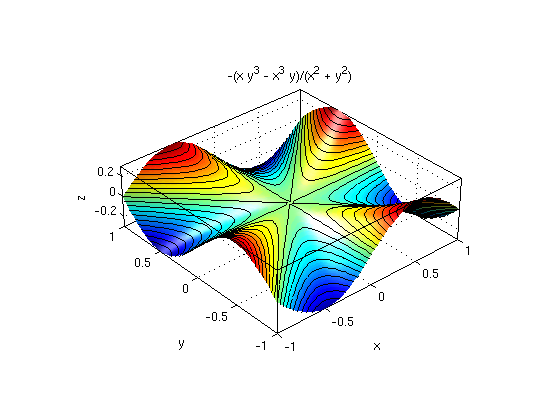
Example where the mixed partial derivatives f_xy and f_yx are NOT equal: f(x,y) = (x^3*y-x*y^3)/(x^2+y^2)

We define f(0,0)=0. Then the function f(x,y) and the partial derivatives f_x, f_y are continuous everywhere.

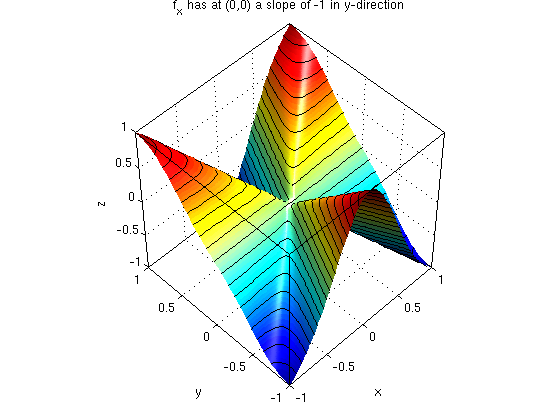
Note that f_x has at (0,0) a slope of -1 in y-direction, hence (f_x)_y(0,0) = -1.

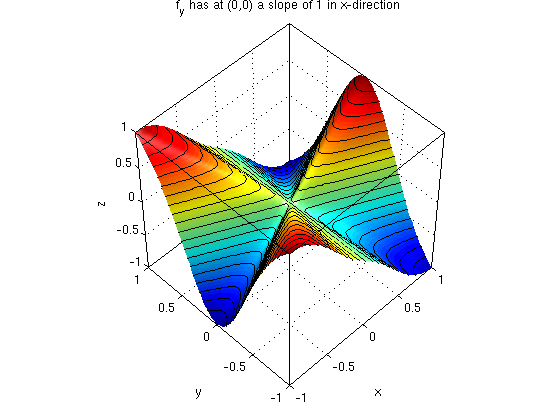
Note that f_y has at (0,0) a slope of 1 in x-direction, hence (f_y)_x(0,0) = 1.

Therefore the two mixed partial derivatives (f_x)_y and (f_y)_x are not equal in the origin.

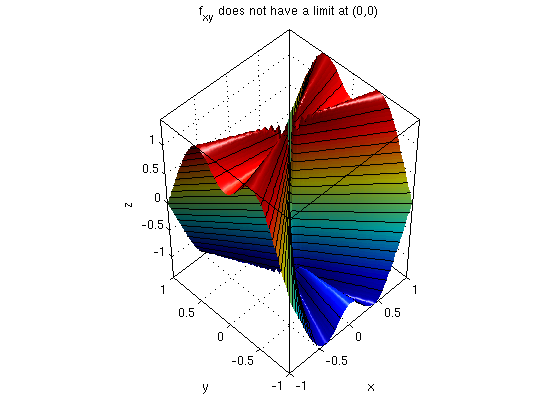
Note that the function (f_x)_y does not have a limit at the origin.

figure(1)
f(x,y) = (x^3*y-x*y^3)/(x^2+y^2);
ezsurf(f,[-1 1 -1 1])
surfcontour; defaultlighting;
nice3d; view(-41,33)

fx = simplify(diff(f,x))      % partial derivative f_x with respect to x
figure(2)
ezsurf(fx,[-1 1 -1 1])
surfcontour; defaultlighting;
nice3d; view(-45,50);
title('f_x has at (0,0) a slope of -1 in y-direction')

fy = simplify(diff(f,y))      % partial derivative f_y with respect to y
figure(3)
ezsurf(fy,[-1 1 -1 1])
surfcontour; defaultlighting;
nice3d; view(-45,50)
title('f_y has at (0,0) a slope of 1 in x-direction')

fxy = simplify(diff(fx,y))    % partial derivative (f_x)_y: first w.r.t. x, then w.r.t. y
figure(4)
ezsurf(fxy,[-1 1 -1 1])
surfcontour; defaultlighting;
nice3d; view(-45,50)
title('f_{xy} does not have a limit at (0,0)')

fx(x, y) =
(y*(x^4 + 4*x^2*y^2 - y^4))/(x^2 + y^2)^2
fy(x, y) =
-(x*(- x^4 + 4*x^2*y^2 + y^4))/(x^2 + y^2)^2
fxy(x, y) =
-(- x^6 - 9*x^4*y^2 + 9*x^2*y^4 + y^6)/(x^2 + y^2)^3

Published with MATLAB® R2013b