Examples Monday, Feb. 24

Contents

Tangent plane for "nice" function

For the function f(x,y) = 5-x^2/2-y^2/4 find for the point (x0,y0)=(1,1) the tangent vectors in x-direction and y-direction. Then plot the tangent plane in this point.

The equation of the tangent plane is z = f(x0,y0) + fx(x0,y0)*(x-x0) + fy(x0,y0)*(y-y0).

Here we obtain the tangent plane z = (17/4) + (-1)*(x-1) + (-1/2)*(y-1).

Note that the tangent plane fits "snugly" onto the surface - this means the function is differentiable at this point.

syms x y real                 % define x,y as real symbolic values
f = 5-x^2/2-y^2/4
fx = diff(f,x)                % partial derivative with respect to x
fy = diff(f,y)                % partial derivative with respect to y
x0 = 1; y0 = 1;
f0 = subs(f,{x,y},{x0,y0})    % substitute (x0,y0) for (x,y)
fx0 = subs(fx,{x,y},{x0,y0})
fy0 = subs(fy,{x,y},{x0,y0})
Tx = [1,0,fx0]                % tangent vector in x-direction
Ty = [0,1,fy0]                % tangent vector in y-direction
N = cross(Tx,Ty)              % normal vector for tangent plane

ezsurf(f,[-2 2 -2 2]); hold on
P = [x0,y0,f0];               % the point on the graph
arrow3(P,Tx); texts(P+Tx,'Tx')
arrow3(P,Ty); texts(P+Ty,'Ty')
arrow3(P,N,'r'); texts(P+N,'N')
plane(P,N)
hold off; nice3d; view(60,20)

f =
- x^2/2 - y^2/4 + 5
fx =
-x
fy =
-y/2
f0 =
17/4
fx0 =
-1
fy0 =
-1/2
Tx =
[ 1, 0, -1]
Ty =
[ 0, 1, -1/2]
N =
[ 1, 1/2, 1]

Tangent plane for "ugly" function

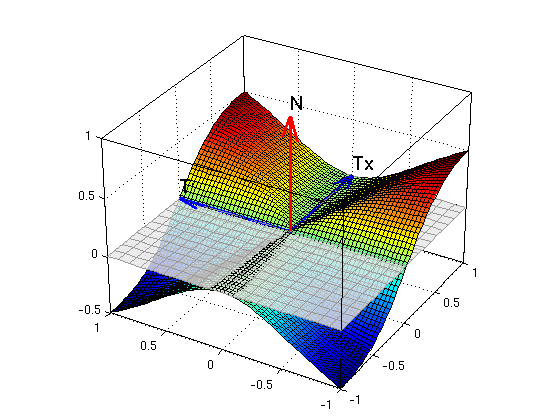
We now consider the function f(x,y) = x*y^2/(x^2+y^2) where we define f(0,0)=0 (we showed in class that this function is continuous). We want to find the tangent plane for the point (x0,y0)=(0,0).

Note that we can't plug in x=0,y=0 in the expressions for f,x,y since we get 0/0.

Here we have f(x0,y0)=0, fx(x0,y0)=0, fy(x0,y0)=0, so the tangent plane at the point (x0,y0)=(0,0) is given by z=0.

Note that the tangent plane does not fit "snugly" onto the surface - this means the function is not differentiable at this point.

f = x*y^2/(x^2+y^2);
ezsurf(f,[-1 1 -1 1])         % plot graph for x=-1...1, y=-1...1
x0 = 0; y0 = 0;
f0 = 0                        % we define f(0,0)=0
fx0 = 0                       % since f(x,0) = 0
fy0 = 0                       % since f(0,y) = 0
Tx = [1,0,fx0]                % tangent vector in x-direction
Ty = [0,1,fy0]                % tangent vector in y-direction
N = cross(Tx,Ty)              % normal vector for tangent plane

ezsurf(f,[-1 1 -1 1]); hold on
nice3d
P = [x0,y0,f0];
arrow3(P,Tx); texts(P+Tx,'Tx')
arrow3(P,Ty); texts(P+Ty,'Ty')
arrow3(P,N); texts(P+N,'N')
plane(P,N)
hold off; nice3d; view(-60,30)

f0 =
     0
fx0 =
     0
fy0 =
     0
Tx =
     1     0     0
Ty =
     0     1     0
N =
     0     0     1

Published with MATLAB® R2013b