Examples Wednesday, March 5
Contents
Gradient and directional derivatives for differentiable function
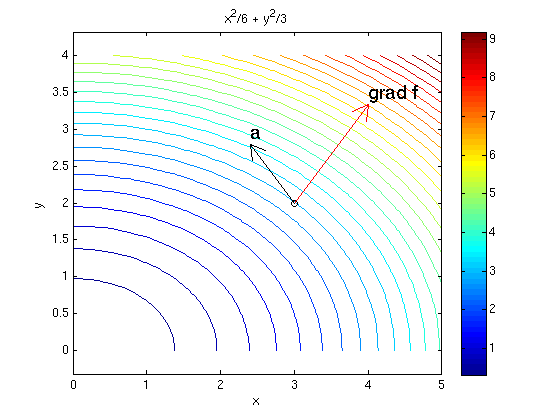
Assume the temperature at the point (x,y) is given by the function f(x,y) = x^2/6 + y^2/3. For the point (x0,y0)=(3,2) find the gradient and the directional derivative for a=(-.6,.8).
syms x y real f = x^2/6 + y^2/3 fx = diff(f,x) % Note: fx is continuous function fy = diff(f,y) % Note: fy is continuous function x0 = 3; y0 = 2; g = subs([fx,fy],{x,y},{x0,y0}) % gradient vector g in point (x0,y0) a = [-.6,.8]; direct_derivative = dot(g,a) % directional derivative D_a f r0 = [x0,y0]; ezcontourc(f,[0,5,0,4],29); colorbar; hold on plotpts(r0,'ko'); arrow(r0,g,'r'); texts(r0+g,'grad f') arrow(r0,a,'k'); texts(r0+a,'a') hold off; axis equal
f = x^2/6 + y^2/3 fx = x/3 fy = (2*y)/3 g = [ 1, 4/3] direct_derivative = 7/15
maximal, minimal and zero values for directional derivative
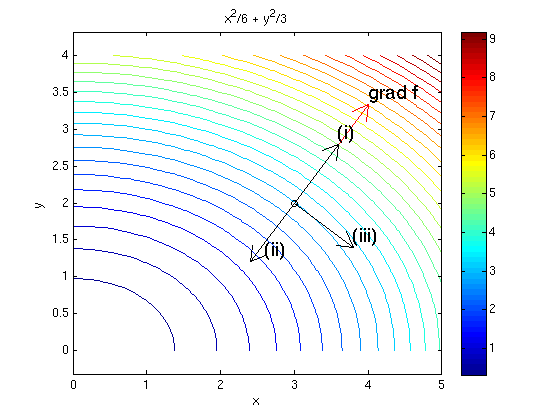
Find a unit vector a such that the directional derivative is (i) maximal, (ii) minimal, (iii) zero. Give the value of the directional derivative in each case.
a_i = g/norm(g) % (i) direct_derivative_i = norm(g) a_ii = -g/norm(g) % (ii) direct_derivative_ii = -norm(g) b = [g(2),-g(1)]; % (iii) a_iii = b/norm(b) % a = -b/norm(b) also works direct_derivative_iii = 0 ezcontourc(f,[0,5,0,4],29); colorbar; hold on plotpts(r0,'ko'); arrow(r0,g,'r'); texts(r0+g,'grad f') arrow(r0,a_i,'k'); texts(r0+a_i,'(i)') arrow(r0,a_ii,'k'); texts(r0+a_ii,' (ii)') arrow(r0,a_iii,'k'); texts(r0+a_iii,'(iii)') hold off; axis equal
a_i =
[ 3/5, 4/5]
direct_derivative_i =
5/3
a_ii =
[ -3/5, -4/5]
direct_derivative_ii =
-5/3
a_iii =
[ 4/5, -3/5]
direct_derivative_iii =
0
Chain rule
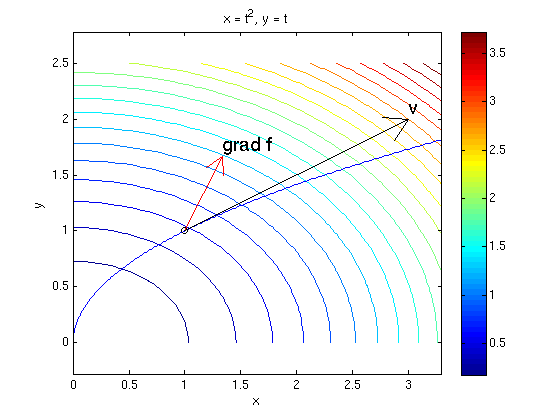
We now move around the plane: our position at time t is r(t) = (X(t),Y(t)) = (t^2,t). Then the temperature at time t is F(t) = f(X(t),Y(t)). Find F'(1) by (i) taking the derivative of F(t), (ii) by using the chain rule.
syms t real t0 = sym(1); X = t^2; Y = t; % we use capital letters for position function F = subs(f,{x,y},{X,Y}) % for x,y substitute X,Y Fp = diff(F,t) % F'(t) derivative_i = subs(Fp,t,t0) % F'(t0) r = [X,Y]; % position function r(t) = (X(t),Y(t)) r0 = subs(r,t,t0) % point r0 for time t0 v = diff(r,t) % velocity vector v0 = subs(v,t,t0) % velocity vector at time t0 g = subs([fx,fy],{x,y},{r0(1),r0(2)}) % gradient of f at point r0 derivative_ii = dot(g,v0) % derivative using chain rule ezcontourc(f,[0,3.3,0,2.5],21); colorbar; hold on ezplot(r(1),r(2),[0 2]); plotpts(r0,'ko'); arrow(r0,g,'r'); texts(r0+g,'grad f') arrow(r0,v0,'k'); texts(r0+v0,'v') hold off; axis equal
F = t^4/6 + t^2/3 Fp = (2*t^3)/3 + (2*t)/3 derivative_i = 4/3 r0 = [ 1, 1] v = [ 2*t, 1] v0 = [ 2, 1] g = [ 1/3, 2/3] derivative_ii = 4/3