Examples Friday, March 7
Contents
Gradient and directional derivatives for differentiable function f(x,y,z)
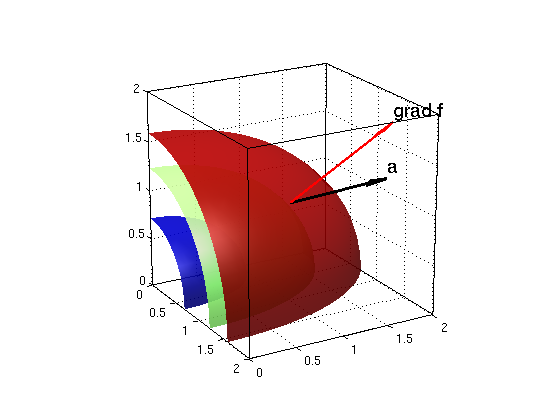
Assume the temperature at the point (x,y,z) is given by the function f(x,y) = x^2/2+y^2/4+z^2/2. For the point (x0,y0,z0)=(1,1,1) find the gradient and the directional derivative for a=(2/3,2/3,1/3).
(You need to download the files defaultlighting.m, Ezplot3.m)
syms x y z real f = x^2/2 + y^2/4 + z^2/2 fx = diff(f,x) % Note: fx, fy, fz are continuous functions fy = diff(f,y) % hence: f is differentiable and fz = diff(f,z) % we can compute directional derivative using gradient x0 = 1; y0 = 1; z0 = 1; g = subs([fx,fy,fz],{x,y,z},{x0,y0,z0}) % gradient vector g in point (x0,y0,z0) a = sym([2/3,2/3,1/3]) direct_derivative = dot(g,a) % directional derivative D_a f ezisosurf(f,[0 2.5 0 2 0 2],[.25 .75 1.25]); hold on r0 = [x0,y0,z0]; arrow3(r0,g,'r'); texts(r0+g,'grad f') arrow3(r0,a,'k'); texts(r0+a,'a') hold off; nice3d; alpha(0.9); view(60,20); defaultlighting
f = x^2/2 + y^2/4 + z^2/2 fx = x fy = y/2 fz = z g = [ 1, 1/2, 1] a = [ 2/3, 2/3, 1/3] direct_derivative = 4/3
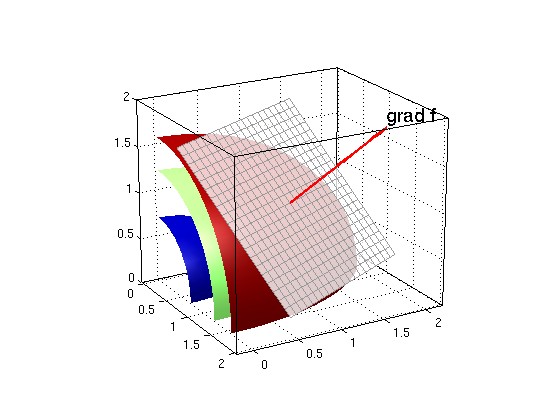
Maximal, minimal values for directional derivative, tangent plane to level surface
Find a unit vector a such that the directional derivative is (i) maximal, (ii) minimal. Give the value of the directional derivative in each case. Plot the tangent plane to the level surface.
a_i = g/norm(g) % (i) direct_derivative_i = norm(g) a_ii = -g/norm(g) % (ii) direct_derivative_ii = -norm(g) ezisosurf(f,[0 2.5 0 2 0 2],[.25 .75 1.25]); hold on arrow3(r0,g,'r'); texts(r0+g,'grad f') plane(r0,g,1,1); % plot tangent plane with gradient as normal vector hold off; nice3d; view(60,20); defaultlighting
a_i = [ 2/3, 1/3, 2/3] direct_derivative_i = 3/2 a_ii = [ -2/3, -1/3, -2/3] direct_derivative_ii = -3/2
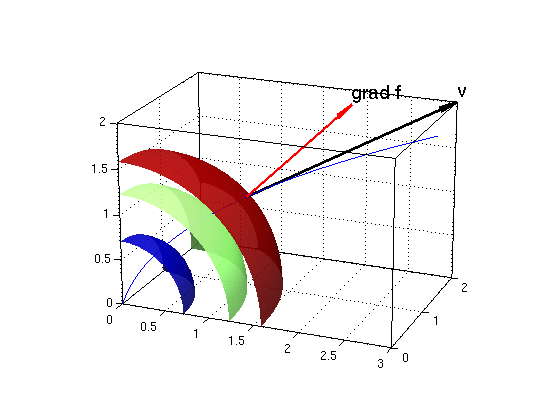
Chain rule for F(t) = f(X(t),Y(t),Z(t))
We now move around in space: our position at time t is r(t) = (X(t),Y(t),Z(t)) = (t^2,t,t). Then the temperature at time t is F(t) = f(X(t),Y(t),Z(t)). Find F'(1) by (i) taking the derivative of F(t), (ii) by using the chain rule.
syms t real t0 = sym(1); X = t^2; Y = t; Z = t; % we use capital letters for position function F = subs(f,{x,y,z},{X,Y,Z}) % for x,y,z substitute X,Y,Z Fp = diff(F,t) % F'(t) derivative_i = subs(Fp,t,t0) % F'(t0) r = [X,Y,Z]; % position function r(t) = (X(t),Y(t),Z(t)) r0 = subs(r,t,t0) % point r0 for time t0 v = diff(r,t) % velocity vector v0 = subs(v,t,t0) % velocity vector at time t0 g = subs([fx,fy,fz],{x,y,z},{r0(1),r0(2),r0(3)}) % gradient of f at point r0 derivative_ii = dot(g,v0) % derivative using chain rule Ezplot3(X,Y,Z,[0 1.7]); hold on % plot curve for t=0...1.7 [xg,yg,zg] = meshgrid(0:.1:2.5,0:.1:2,0:.1:2); F = xg.^2/2 + yg.^2/4 + zg.^2/2; isosurf(xg,yg,zg,F,0.25); % plot level surface for f=.25 isosurf(xg,yg,zg,F,0.75); % plot level surface for f=.75 isosurf(xg,yg,zg,F,1.25); % plot level surface for f=1.25 r0 = [x0,y0,z0]; arrow3(r0,g,'r'); texts(r0+g,'grad f') arrow3(r0,v0,'k'); texts(r0+v0,'v') hold off; nice3d; alpha(0.9); view(22,20); defaultlighting
F = t^4/2 + (3*t^2)/4 Fp = 2*t^3 + (3*t)/2 derivative_i = 7/2 r0 = [ 1, 1, 1] v = [ 2*t, 1, 1] v0 = [ 2, 1, 1] g = [ 1, 1/2, 1] derivative_ii = 7/2