Examples Monday, March 10: Find maximum and minimum of f(x,y) on a region R
Contents
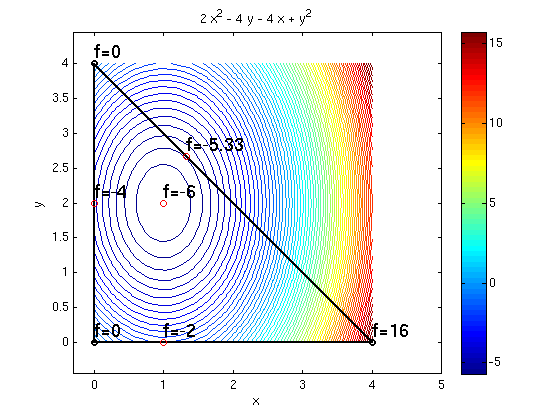
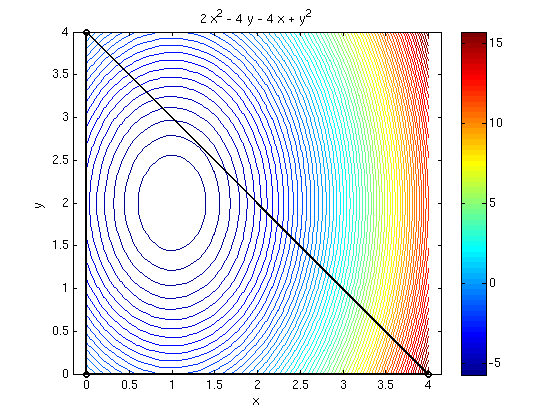
Contour plot of function f(x,y)
The region R is the triangle with corners (0,0), (4,0), (0,4) (contains interior and boundary of triangle).
Consider the function f(x,y)=2*x^2-4*x+y^2-4*y on R.
Make a contour of the function and also show the triangle.
syms x y real f = 2*x^2-4*x+y^2-4*y ezcontourc(f,[0 4 0 4],70); % make contour plot of f for x in [0,4], y in [0,4] colorbar; hold on A = [0,0]; B=[4,0]; C=[0,4]; % corners of the triangle plotpts([A;B;C;A],'ko-','Linewidth',2); % plot corners and sides of triangle hold off; axis equal;
f = 2*x^2 - 4*x + y^2 - 4*y
(1) Find the critical points in the interior of R
We see that there is one critical point P0=(1,2) with function value -6.
fx = diff(f,x) fy = diff(f,y) [xs,ys] = solve(fx,fy,x,y); % Find all points xs,ys where fx=0 and fy=0 P0 = [xs,ys] % here: one solution point P0 f0 = subs(f,{x,y},{xs,ys}) % with function value f0
fx = 4*x - 4 fy = 2*y - 4 P0 = [ 1, 2] f0 = -6
(2) f on the boundary: corners
At the three corners A,B,C we have function values 0, 16, 0.
fA = subs(f,{x,y},[0,0]) % Evaluate f in the three corners
fB = subs(f,{x,y},[4,0])
fC = subs(f,{x,y},[0,4])
fA = 0 fB = 16 fC = 0
(2) f on side 1: (x,0) with x in [0,4]
On side 1 we have a critical point P1=[1,0] with function value -2.
g1 = subs(f,{x,y},{x,0}) % g1(x) is f on side 1
g1p = diff(g1,x) % g1'(x)
xs = solve(g1p,x) % find xs such that g1'(x)=0
P1 = [xs,0] % here: one solution point P1
f1 = subs(f,{x,y},{xs,0}) % with function value f1
g1 = 2*x^2 - 4*x g1p = 4*x - 4 xs = 1 P1 = [ 1, 0] f1 = -2
(2) f on side 2: (0,y) with y in [0,4]
On side 2 we have a critical point P2=[0,2] with function value -4.
g2 = subs(f,{x,y},{0,y}) % g2(y) is f on side 2
g2p = diff(g2,y) % g2'(y)
ys = solve(g2p,y) % find ys such that g2'(y)=0
P2 = [0,ys] % here: one solution point P2
f2 = subs(f,{x,y},{0,ys}) % with function value f2
g2 = y^2 - 4*y g2p = 2*y - 4 ys = 2 P2 = [ 0, 2] f2 = -4
(2) f on side 3: (x,4-x) with x in [0,4]
On side 3 we have a critical point P3=[4/3,8/3] with function value -16/3.
g3 = subs(f,{x,y},{x,4-x}) % g3(x) is f on side 3
g3p = diff(g3,x) % g3'(x)
xs = solve(g3p,x) % find xs such that g3'(x)=0
P3 = [xs,4-xs] % here: one solution point P3
f3 = subs(f,{x,y},{xs,4-xs}) % with function value f3
g3 = (x - 4)^2 + 2*x^2 - 16 g3p = 6*x - 8 xs = 4/3 P3 = [ 4/3, 8/3] f3 = -16/3
(3) Find maximum and minimum of f on triangle
We take the maximum and minimum of the function values computed so far:
The maximum of f on the triangle is 16 which occurs for (x,y)=B=(4,0).
The minimum of f on the triangle is -6 which occurs for (x,y)=P0=(1,2).
maximum = max(double([f0,fA,fB,fC,f1,f2,f3])) % maximum of f on triangle minimum = min(double([f0,fA,fB,fC,f1,f2,f3])) % minimum of f on triangle ezcontourc(f,[0 4 0 4],70); % make contour plot of f for x in [0,4], y in [0,4] colorbar; hold on A = [0,0]; B=[4,0]; C=[0,4]; % corners of the triangle plotpts([A;B;C;A],'ko-','Linewidth',2); % plot corners and sides of triangle plotpts([P0;P1;P2;P3],'ro'); % mark critical points with red circles texts(A,'f=0') texts(B,'f=16') texts(C,'f=0') texts(P0,'f=-6') texts(P1,'f=-2'); texts(P2,'f=-4'); texts(P3,'f=-5.33') hold off; axis([-.3 5 0 4]); axis equal;
maximum =
16
minimum =
-6