Examples Wednesday, March 12: Second Partials Test
Contents
You need to download new m-files.
Download the files defaultlighting.m, surfcontour.m.
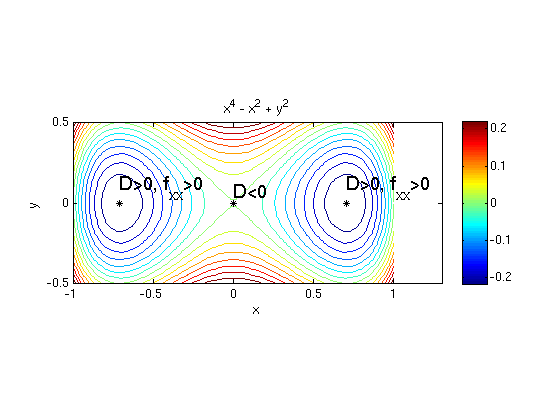
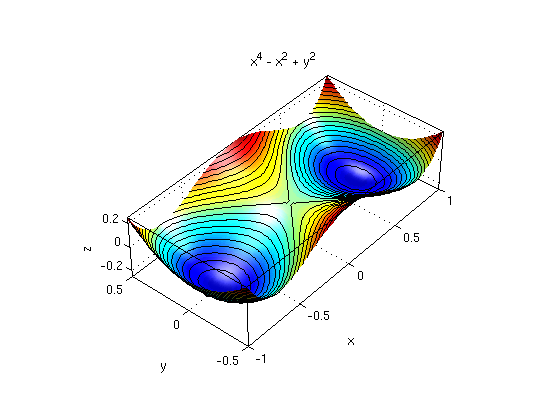
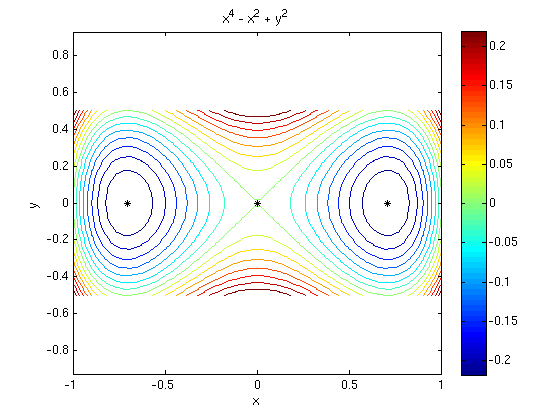
(a) Find all critical points of the function f(x,y) = x^4 - x^2 + y^2.
Answer: We find three critical points (0,0), (1/sqrt(2),0), (-1/sqrt(2),0).
syms x y real f = x^4 - x^2 + y^2; fx = diff(f,x) fy = diff(f,y) [xs,ys] = solve(fx,fy,x,y); [xs,ys] % Find all points (xs,ys) where fx=0, fy=0 figure(1); % Figure 1: surface plot ezsurf(f,[-1 1 -.5 .5]); surfcontour; defaultlighting; % add contours, lighting nice3d; view(-50,40) figure(2) % Figure 2: contour plot, mark critical points ezcontourc(f,[-1 1 -.5 .5],15); colorbar; axis equal; hold on plotpts([xs,ys],'k*') % mark critical points with black asterisks
fx = 4*x^3 - 2*x fy = 2*y ans = [ 0, 0] [ 2^(1/2)/2, 0] [ -2^(1/2)/2, 0]
(b) Use the second partials test to classify the critical points.
Answer: (0,0) is a saddle point, the other two critical points are relative minima.
fxx = diff(fx,x) % find all second partial derivatives fxy = diff(fx,y) fyy = diff(fy,y) D = fxx*fyy - fxy^2 % discriminant % find [D,fxx] for each critical point subs([D,fxx],{x,y},{xs(1),ys(1)}) % D<0: saddle point subs([D,fxx],{x,y},{xs(2),ys(2)}) % D>0, fxx>0: rel. minimum subs([D,fxx],{x,y},{xs(3),ys(3)}) % D>0, fxx>0: rel. minimum ezcontourc(f,[-1 1 -.5 .5],15); colorbar; axis equal; hold on plotpts([xs,ys],'k*') texts([xs(1),ys(1)],'D<0') texts([xs(2),ys(2)],'D>0, f_{xx}>0') texts([xs(3),ys(3)],'D>0, f_{xx}>0') axis([-1 1.3 -.5 .5]); hold off
fxx = 12*x^2 - 2 fxy = 0 fyy = 2 D = 24*x^2 - 4 ans = [ -4, -2] ans = [ 8, 4] ans = [ 8, 4]