Examples Friday, March 14: Lagrange Multipliers for f(x,y,z)
Contents
(a)
We want to build a box where the edges have length x,y,z. We want to have x+y+z=12. What is the largest volume V=x*y*z which we can achieve?
In other words, we want to find the maximum of the function f(x,y,z)=x*y*z, subject to the constraint x+y+z=12.
Answer: The maximum volume of the box is 64, for the values (x,y,z)=(4,4,4).
syms x y z lambda real f = x*y*z; g = x + y + z - 12; % we define g(x,y) so that the constraint is g(x,y)=0 fx = diff(f,x) fy = diff(f,y) fz = diff(f,z) gx = diff(g,x) gy = diff(g,y) gz = diff(g,z) % We obtain a system of 4 equations for 4 unknowns x,y,z,lambda s = solve(fx-lambda*gx,fy-lambda*gy,fz-lambda*gz,g,x,y,z,lambda); % solve the system [s.x,s.y,s.z] % s.x, s.y, s.z are vectors with x,y,z values % here we get four solutions fs = subs(f,{x,y,z},{s.x,s.y,s.z}) % plug each solution in function f % fs is vector of four function values % Matlab can't find max/min of symbolic values, so we need "double" to convert to machine numbers fsd = double(fs); fmax = max(fsd) % maximum fmin = min(fsd) % minimum
fx =
y*z
fy =
x*z
fz =
x*y
gx =
1
gy =
1
gz =
1
ans =
[ 12, 0, 0]
[ 0, 0, 12]
[ 0, 12, 0]
[ 4, 4, 4]
fs =
0
0
0
64
fmax =
64
fmin =
0
(b)
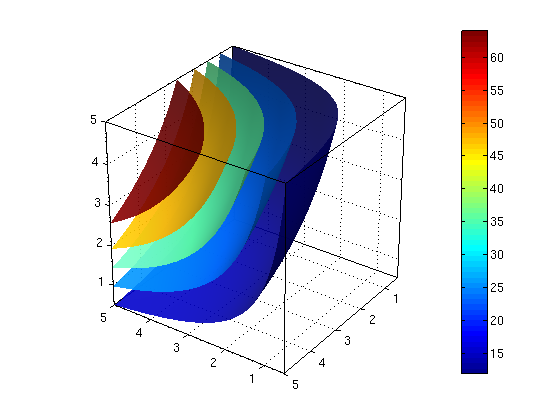
Make a plot of the level sets (surfaces) of the function f.
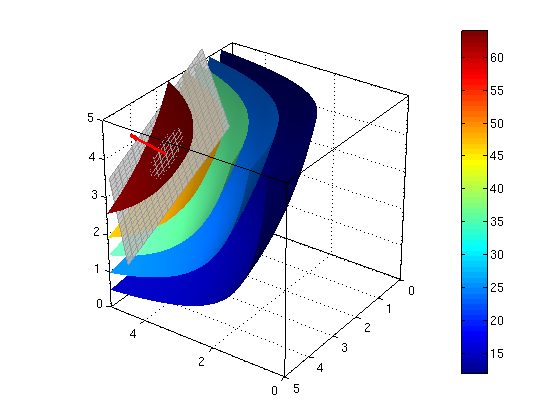
Make a second plot which also shows the plane x+y+z=12, together with the location of the maximum.
Note that the plane is tangent to the level set f(x,y,z)=64 at the location (4,4,4) of the maximum.
figure(1) ezisosurf(f,[0 5 0 5 0 5],[12,24,36,48,64]); % plot surfaces for f=12,24,36,48,64 colorbar; alpha(0.9); nice3d; view(-145,30); defaultlighting; figure(2) ezisosurf(f,[0 5 0 5 0 5],[12,24,36,48,64]); hold on plane([4,4,4],[1,1,1],2,2) % surface g=0 is plane colorbar; hold off; nice3d; axis([0 5 0 5 0 5]); view(-145,30); defaultlighting;