Examples Monday, March 24: Double Integrals
Contents
You need to download new m-files.
Download the files regionvs.m, regionhs.m, ezsurfvs.m, ezsurfhs.m
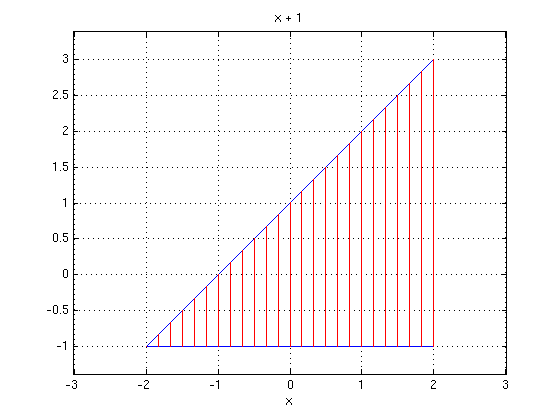
(a) Region R as vertically simple region
The region R is the triangle (interior and boundary) with vertices (-2,-1), (2,-1), (2,3).
Is this region vertically simple? If yes, find a,b and g1(x), g2(x).
Answer: Yes, the region R is vertically simple: each intersection with a vertical line at x gives an interval [g1(x),g2(x)] for y.
Here we have -2 <= x <= 2 and -1 <= y <= x+1. This means we have a=-2, b=2, g1(x)=-1, g2(x)=x+1.
syms x y a = -2; b = 2; g1 = -1; g2 = x+1; regionvs(a,b,g1,g2) % draw Vertically Simple region given by a,b,g1,g2 axis equal; grid on
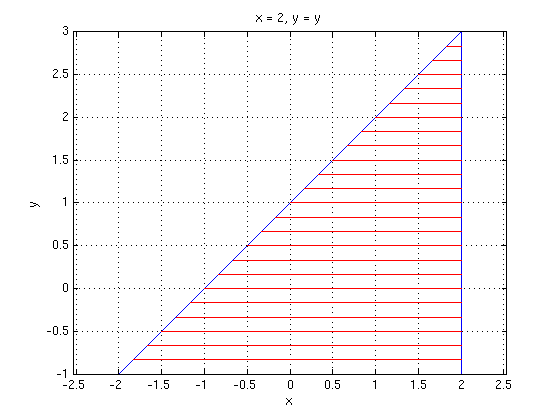
(b) Region R as horizontally simple region
Is this region R horizontally simple? If yes, find c,d and h1(y), h2(y).
Answer: Yes, the region R is horizontally simple: each intersection with a horizontal line at y gives an interval [h1(y),h2(y)] for x.
Here we have -1 <= y <= 3 and y-1 <= x <= 2. This means we have c=-1, d=3, h1(y)=y-1, h2(y)=2.
syms x y c = -1; d = 3; h1 = y-1; h2 = 2; regionhs(c,d,h1,h2) % draw Horizontally Simple region given by c,d,h1,h2 axis equal; grid on
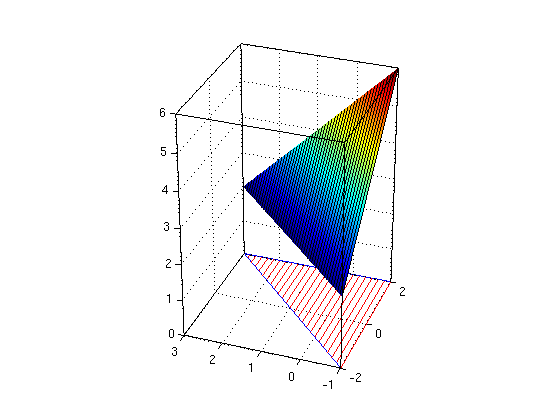
(c) Find the double integral, inner integral over y
Let f(x,y)=3+x-y. Find the double integral of the function f over the region R as follows: First find the integral A(x) for a slice at x. Then integrate over the function A(x).
Answer: We need to specify R as a vertically simple region. Then A(x) is the integral of f(x,y) from y=g1(x) to y=g2(x). The double integral I is obtained as integral of A(x) from x=a to b.
f = 3+x-y A = int(f,y,g1,g2) I = int(A,x,a,b) ezsurfvs(f,a,b,g1,g2); hold on % draw graph of f over R (ezsurfvs is for Vertically Simple region) regionvs(a,b,g1,g2) % draw vertically simple region R hold off; nice3d; view(-70,30)
f = x - y + 3 A = ((x + 2)*(x + 6))/2 I = 80/3
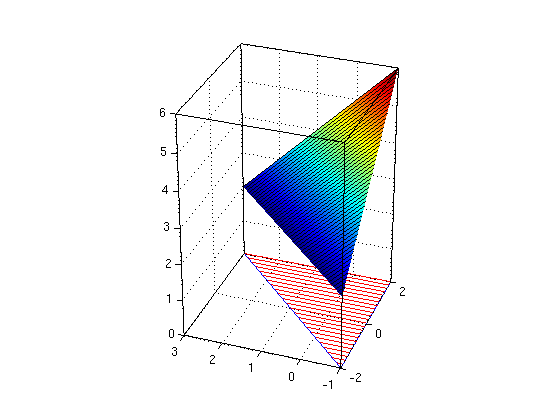
(d) Find the double integral, inner integral over x
Find the double integral of the function f over the region R as follows: First find the integral A(y) for a slice at y. Then integrate over the function A(y).
Answer: We need to specify R as a horizontally simple region. Then A(y) is the integral of f(x,y) from x=h1(y) to x=h2(y). The double integral I is obtained as integral of A(y) from y=c to d.
A = int(f,x,h1,h2) I = int(A,y,c,d) % gives same result as in (c) ! ezsurfhs(f,c,d,h1,h2); hold on % draw graph of f over R (ezsurfhs is for Horizontally Simple region) regionhs(c,d,h1,h2) % draw horizontally simple region R hold off; nice3d; view(-70,30)
A = ((y - 3)*(y - 7))/2 I = 80/3