Examples from class on Wednesday, Jan. 29

(a)

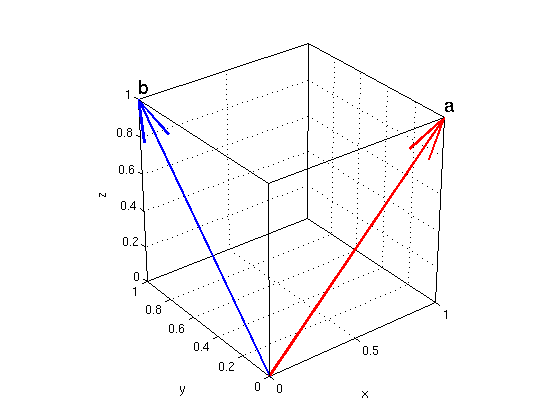
Find the angle between the vectors a=(1,0,1) and b=(0,1,1).

a = sym([1,0,1]); b = sym([0,1,1]);   % use symblic vectors for exact answer
Q = dot(a,b)/(norm(a)*norm(b))
angle = acos(Q)                       % answer is pi/3 = 60 degrees

or = [0,0,0];
arrow3(or,a,'r'); hold on; texts(a,'a')
arrow3(or,b,'b'); texts(b,'b')
nice3d; axis([0 1 0 1 0 1])
hold off

Q =
1/2
angle =
pi/3

(b)

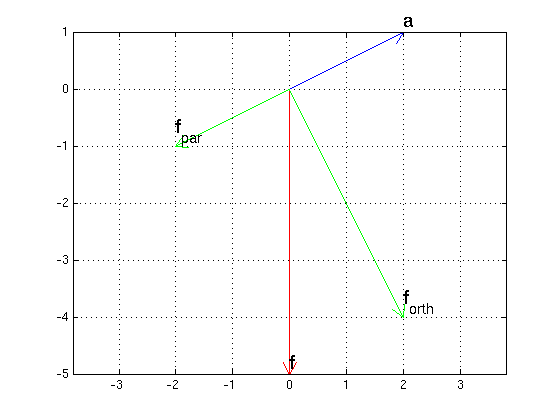
Let a = (2,1). Decompose the vector f = (0,-5) as f = f_par + f_orth where f_par is parallel to a, and f_orth is orthogonal to a.

a = [2,1]; f = [0,-5];
f_par = dot(a,f)/dot(a,a)*a            % projection of vector f onto vector a
f_orth = f - f_par

or = [0,0];
arrow(or,f,'r'); hold on; texts(f,'f')
arrow(or,a,'b'); texts(a,'a')
arrow(or,f_par,'g'); texts(f_par,'f_{par}')
arrow(or,f_orth,'g'); texts(f_orth,'f_{orth}')
hold off
axis equal; grid on

f_par =
    -2    -1
f_orth =
     2    -4

Examples from class on Wednesday, Jan. 29

Contents

(a)

(b)