Examples Wednesday, March 26: Double integrals in polar coordinates
Contents
You need to download new m-files.
Download the files regionpol.m, ezsurfpol.m
(a) Describe region R with alpha, beta, h1, h2
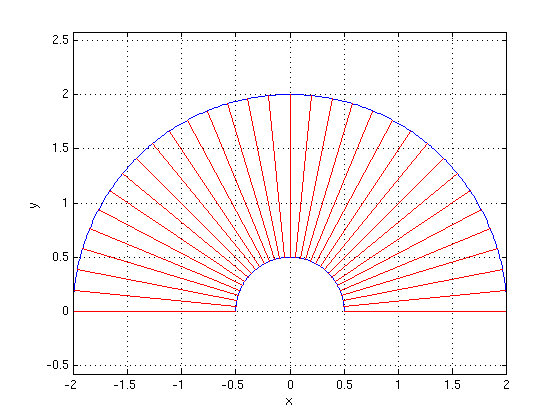
The region R consists of the points (x,y) with 1/4<=x^2+y^2<= 4 and y>=0. Find alpha, beta, h1, h2 for this region.
Answer: We have alpha=0, beta=pi, h1=1/2, h2=2.
syms theta regionpol(0,pi,1/2,2) axis equal; grid on
(b) Describe region R with alpha, beta, h1, h2
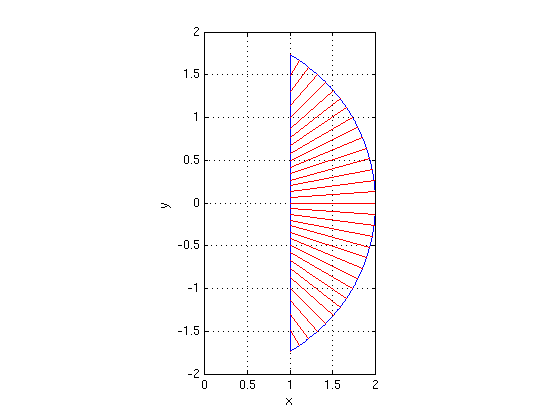
The region R consists of the points (x,y) with x^2+y^2<= 4 and x>=1. Find alpha, beta, h1, h2 for this region.
Answer:
The intersection of the circle x^2+y^2=4 and the line x=1 consists of two points (1,-sqrt(3)) and (1,sqrt(3)), corresponding to theta=-pi/3 and theta=pi/3.
For x=1 we have r*cos(theta)=1, hence r=1/cos(theta).
Therefore we get alpha=-pi/3, beta=pi/3, h1=1/cos(theta), h2=2.
syms theta regionpol(-pi/3,pi/3,1/cos(theta),2) axis equal; axis([0 2 -2 2]); grid on
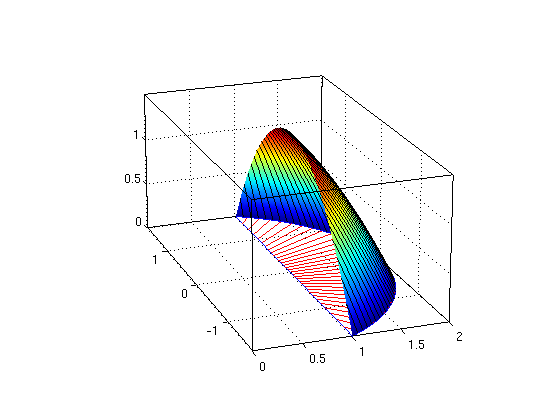
(c) Integrate the function f(x,y) = 2-(x^2+y^2)/2 over the region R from (a).
First find the inner integral A(theta) by integrating over r. Then find the double integral I by integrating A(theta) over theta.
syms r theta Pi = sym('pi'); % symbolic pi alpha = 0; beta = Pi; h1 = 1/2; h2 = 2; F = 2 - r^2/2 % f expressed in polar coordinates A = int(F,r,h1,h2) % A(theta) is inner integral over r I = int(A,theta,alpha,beta) ezsurfpol(F,alpha,beta,h1,h2); hold on % draw graph regionpol(alpha,beta,h1,h2); hold off % draw region in xy-plane nice3d; view(15,37)
F = 2 - r^2/2 A = 27/16 I = (27*pi)/16
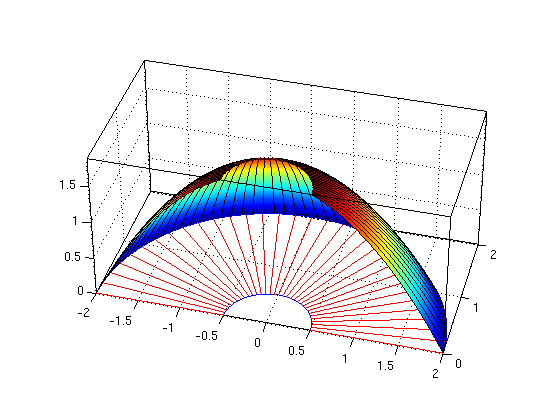
(d) Integrate the function f(x,y) = 2-(x^2+y^2)/2 over the region R from (b).
First find the inner integral A(theta) by integrating over r. Then find the double integral I by integrating A(theta) over theta (this integral is difficult to do by hand).
syms r theta Pi = sym('pi'); % symbolic pi alpha = -Pi/3; beta = Pi/3; h1 = 1/cos(theta); h2 = 2; F = 2 - r^2/2 % f expressed in polar coordinates A = int(F,r,h1,h2) % A(theta) is inner integral over r I = int(A,theta,alpha,beta) ezsurfpol(F,alpha,beta,h1,h2); hold on % draw graph regionpol(alpha,beta,h1,h2); hold off % draw region in xy-plane nice3d; xlim([0 2]); view(-20,20)
F = 2 - r^2/2 A = 8/3 - (2*cos(theta)^2 - 1/6)/cos(theta)^3 I = (16*pi)/9 + log(3^(1/2) + 2)/6 - log(56*3^(1/2) + 97) + 3^(1/2)/3