Examples: Evaluate triple integrals in Cartesian, cylindrical, spherical coordinates
Contents
You need to download new m-files.
Download the files regionvs.m, ezsurfvs.m, regionpol.m, ezsurfpol.m, defaultlighting.m
(1a): Triple integral in Cartesian coordinates x,y,z
The region D consists of the points (x,y,z) with x^2+y^2+z^2<=4 and x^2+y^2<=1 and z>=0. Find the volume of this region.
Answer: Note that x^2+y^2+z^2<=4 gives points inside of a sphere with radius 2, and x^2+y^2<=1 gives points inside a cylinder of radius 1. We have -1<=x<=1, -sqrt(1-x^2)<=y<=sqrt(1-x^2), 0<=z<=sqrt(4-x^2-y^2).
syms x y z real f = 1; a = -1; b = 1; % limits for x g1 = -sqrt(1-x^2); g2 = sqrt(1-x^2); % limits for y h1 = 0; h2 = sqrt(4-x^2-y^2); % limits for z I1 = int(f,z,h1,h2) % z integral: this is easy I2 = int(I1,y,g1,g2) % y-integral: Matlab can do this I = int(I2,x,a,b) % z-integral: Matlab cannot do this, returns int(...) Id = double(I) % we can still find numerical value using double(...) or vpa(...) ezsurfvs(h2,a,b,g1,g2); hold on % draw upper surface regionvs(a,b,g1,g2); hold off % draw region R in xy-plane nice3d; view(-40,20); defaultlighting;
I1 =
(- x^2 - y^2 + 4)^(1/2)
I2 =
3^(1/2)*(1 - x^2)^(1/2) - 2*asin((1 - x^2)^(1/2)/(4 - x^2)^(1/2))*(x^2/2 - 2)
I =
int(3^(1/2)*(1 - x^2)^(1/2) - 2*asin((1 - x^2)^(1/2)/(4 - x^2)^(1/2))*(x^2/2 - 2), x == -1..1)
Id =
5.8724

(1b): Triple integral in cylindrical coordinates r,theta,z
Compute the integral from 1(a) using cylindrical coordinates
Answer: We have 0<=theta<=2*pi, 0<=r<=1, 0<=z<=sqrt(4-r^2)
% Compute the integral from 1(a) using cylindrical coordinates % *Answer:* We have 0<=theta<=2*pi, 0<=r<=1, 0<=z<=sqrt(4-r^2) syms r theta z real f = 1; % integral f*r*dr*dtheta*dz Pi = sym('pi'); a = 0; b = 2*Pi; % limits for theta G1 = 0; G2 = 1; % limits for r H1 = 0; H2 = sqrt(4-r^2); % limits for z I1 = int(f*r,z,H1,H2) % z integral: this is easy I2 = int(I1,r,G1,G2) % r-integral I = int(I2,theta,a,b) % theta-integral Id = double(I) % we get same result as in (1a) ! ezsurfpol(H2,a,b,G1,G2); hold on % draw upper surface regionpol(a,b,G1,G2); hold off % draw region R in xy-plane nice3d; view(-40,20); defaultlighting;
I1 =
r*(4 - r^2)^(1/2)
I2 =
8/3 - 3^(1/2)
I =
-2*pi*(3^(1/2) - 8/3)
Id =
5.8724
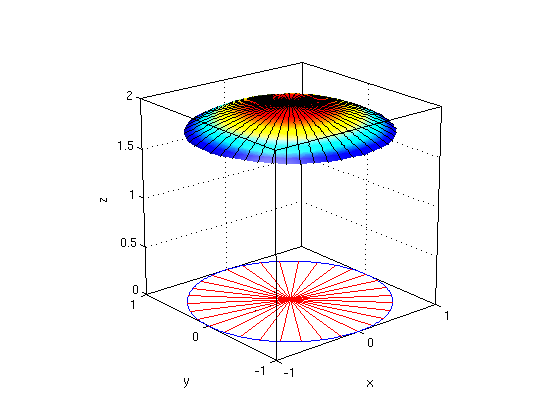
(2a): Triple integral in cylindrical coordinates r,theta,z
Now the region D consists of the points (x,y,z) with x^2+y^2+z^2<=4 and z>=sqrt(3)*r. Find the volume of this region.
Answer: Note that x^2+y^2+z^2<=4 gives points inside of a sphere with radius 2, and z>=sqrt(3)*r gives points in a cone.
We have 0<=theta<=2*pi, 0<=r<=1, sqrt(3)*r<=z<=sqrt(4-r^2)
syms r theta z real f = 1; % integral f*r*dr*dtheta*dz Pi = sym('pi'); a = 0; b = 2*Pi; % limits for theta G1 = 0; G2 = 1; % limits for r H1 = sqrt(3)*r; H2 = sqrt(4-r^2); % limits for z I1 = int(f*r,z,H1,H2) % z integral I2 = int(I1,r,G1,G2) % r-integral I = int(I2,theta,a,b) % theta-integral Id = double(I) ezsurfpol(H1,a,b,G1,G2); hold on % draw lower surface ezsurfpol(H2,a,b,G1,G2); % draw upper surface regionpol(a,b,G1,G2); hold off % draw region R in xy-plane nice3d; view(-40,20); defaultlighting;
I1 =
-r*(3^(1/2)*r - (4 - r^2)^(1/2))
I2 =
8/3 - (4*3^(1/2))/3
I =
-(8*pi*(3^(1/2) - 2))/3
Id =
2.2448
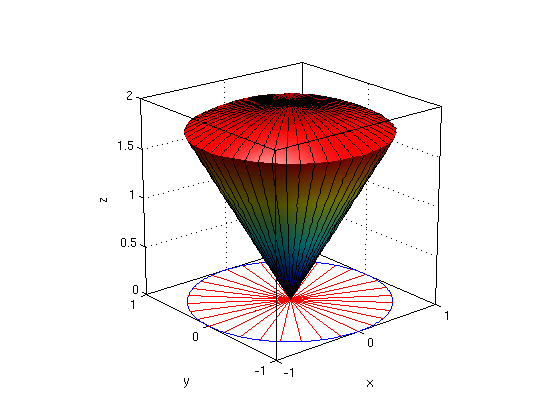
(2b): Triple integral in spherical coordinates rho,phi,theta
For the region D from the previous problem find the volume using spherical coordinates.
Answer: On the boundary of the cone we have z=sqrt(3)*r. Since r/z=tan(phi) we have phi=arctan(1/sqrt(3))=pi/6 on the boundary of the cone.
Hence we have 0<=theta<=2*pi, 0<=phi<=pi/6, 0<=rho<=2
syms rho phi theta real Pi = sym('pi'); f = 1; % integral f*rho^2*sin(phi)*drho*dphi*dtheta a = 0; b = 2*Pi; % limits for theta h1 = 0; h2 = Pi/6; % limits for phi F1 = 0; F2 = 2; % limits for rho I1 = int(f*rho^2*sin(phi),rho,F1,F2) % z integral I2 = int(I1,phi,h1,h2) % phi-integral I = int(I2,theta,a,b) % theta-integral Id = double(I) % we get same result as in (2a) !
I1 =
(8*sin(phi))/3
I2 =
8/3 - (4*3^(1/2))/3
I =
-(8*pi*(3^(1/2) - 2))/3
Id =
2.2448