Examples: Triple integrals in spherical coordinates, center of mass
Contents
(1): Region D bounded by a sphere and two planes
The region D consists of the points (x,y,z) with x^2+y^2+z^2<=4 and y>=0, z>=1
Describe this region in spherical coordinates alpha<=theta<=beta, h1<=phi<=h2, H1<=rho<=H2 and plot it.
Answer: The region y>=0 corresponds to 0<=theta<=pi. Let r=sqrt(x^2+y^2). At the intersection of the plane and the sphere we have r^2+1^2=4, so r=sqrt(3). Since r/z=tan(phi) we have phi=arctan(sqrt(3))=pi/3 on this intersection. As z=rho*cos(phi) we have on the plane z=1 that rho=1/cos(phi).
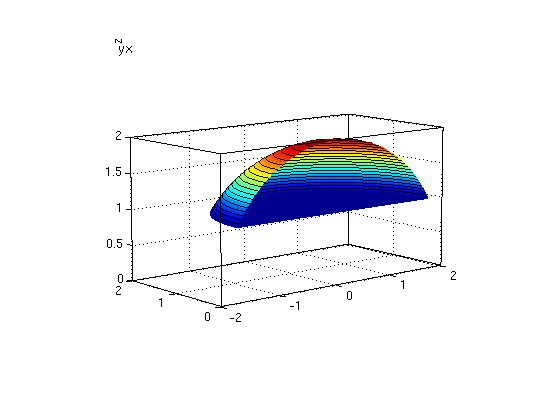
Hence we have 0<=theta<=2*pi, 0<=phi<=pi/3, 1/cos(phi)<=rho<=2.
syms rho phi theta z real Pi = sym('pi'); a=0; b=Pi; % limits for theta h1=0; h2=Pi/3; % limits for phi F1=1/cos(phi); F2=2; % limits for rho ezsurfspher(F2,a,b,h1,h2); hold on % draw upper surface surfcontour % show contours instead of grid ezsurfspher(F1,a,b,h1,h2); % draw lower surface surfcontour hold off; nice3d; axis([-2 2 0 2 0 2]); view(-40,10);
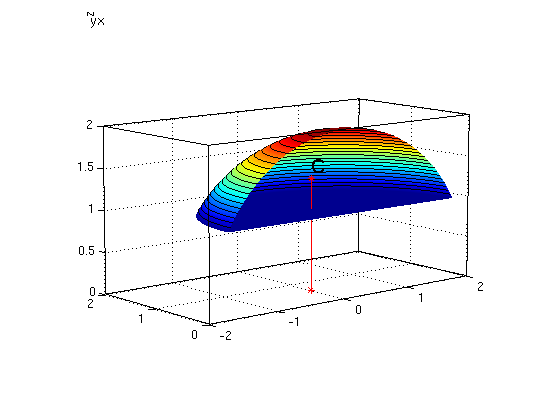
(2): Find the volume V and center of mass of the region D using spherical coordinates
X = rho*sin(phi)*cos(theta); % express x,y,z in spherical coordinates Y = rho*sin(phi)*sin(theta); Z = rho*cos(phi); J = rho^2*sin(phi) % volume element is rho^2*sin(phi)*drho*dphi*dtheta % Find volume: integrate over 1*dV = 1*J*drho*dphi*dtheta: V = int(int(int(1*J,rho,F1,F2),phi,h1,h2),theta,a,b) % Find integral of x*dV: Ix = int(int(int(X*J,rho,F1,F2),phi,h1,h2),theta,a,b) % Find integral of y*dV: Iy = int(int(int(Y*J,rho,F1,F2),phi,h1,h2),theta,a,b) % Find integral of z*dV: Iz = int(int(int(Z*J,rho,F1,F2),phi,h1,h2),theta,a,b) C = [Ix,Iy,Iz]/V; % center of mass center = double(C) % numerical values C0 = [C(1),C(2),0]; ezsurfspher(F2,a,b,h1,h2); hold on % draw upper surface surfcontour ezsurfspher(F1,a,b,h1,h2); % draw lower surface surfcontour plotpts([C;C0],'r*-'); texts(C,'C') hold off; nice3d; axis([-2 2 0 2 0 2]); view(-40,10)
J =
rho^2*sin(phi)
V =
(5*pi)/6
Ix =
0
Iy =
(4*pi)/3 - (3*3^(1/2))/2
Iz =
(9*pi)/8
center =
0 0.6076 1.3500