Examples: Change of variables
Contents
(1) Double integral: polar coordinates
For polar coordinates (r,theta) find the area element using the determinant.
Answer: dx*dy = J*dr*dtheta with J = r
syms r theta real X = r*cos(theta) % We use capital letters for the functions X(rho,phi,theta) etc. Y = r*sin(theta) M = jacobian([X,Y],[r,theta]) % 2 by 2 matrix of all partial derivatives % 1st row are derivatives of X, 2nd row derivatives of Y J = simplify(det(M)) % find determinant and simplify
X = r*cos(theta) Y = r*sin(theta) M = [ cos(theta), -r*sin(theta)] [ sin(theta), r*cos(theta)] J = r
(2a) Double integral: Plot region R given in terms of u,v
Let X(u,v)=u/v and Y(u,v)=v. The region R consists of the points (X,Y) where 1<=u<=3 and sqrt(u)<=v<=sqrt(2*u).
Plot the region R in the xy-plane.
syms u v real X = u/v; Y = v; Z = 0; ezsurfpar(X,Y,Z,1,3,sqrt(u),sqrt(2*u)) % plot points (X,Y,0) for 1<=u<=3, sqrt(u)<=v<=sqrt(2*u) view(0,90) % and look vertically down at xy-plane
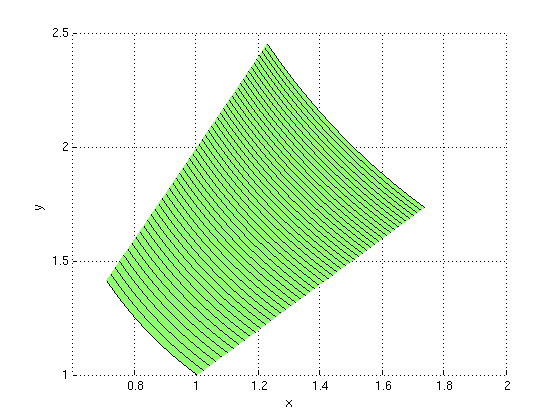
(2b) Double integral: Find integral over region R using u,v variables
Let f(x,y) = x^3*y and find the integral I of the function f over the region R, using the variables u,v.
syms x y real f = x^3*y F = subs(f,{x,y},{X,Y}) % substitute X,Y from above for x,y to get F(u,v) M = jacobian([X,Y],[u,v]) % Find 2 by 2 matrix of partial derivatives % M = [ X_u X_v ; Y_u Yv ] J = det(M) % determinant I1 = int(F*J,v,sqrt(u),sqrt(2*u)) % inner integral over v I = int(I1,u,1,3) % outer integral over u
f = x^3*y F = u^3/v^2 M = [ 1/v, -u/v^2] [ 0, 1] J = 1/v I1 = u^2/4 I = 13/6
(3) Triple integral: volume element for spherical coordinates
For spherical coordinates (rho,phi,theta) find the volume element using the determinant.
Answer: dx*dy*dz = J*drho*dphi*dtheta with J = rho^2*sin(phi)
syms rho phi theta real X = rho*sin(phi)*cos(theta) % We use capital letters for the functions X(rho,phi,theta) etc. Y = rho*sin(phi)*sin(theta) Z = rho*cos(phi) M = jacobian([X,Y,Z],[rho,phi,theta]) % 3 by 3 matrix of all partial derivatives % 1st row are derivatives of X, 2nd row derivatives of Y etc. J = simplify(det(M)) % find determinant and simplify
X = rho*cos(theta)*sin(phi) Y = rho*sin(phi)*sin(theta) Z = rho*cos(phi) M = [ cos(theta)*sin(phi), rho*cos(phi)*cos(theta), -rho*sin(phi)*sin(theta)] [ sin(phi)*sin(theta), rho*cos(phi)*sin(theta), rho*cos(theta)*sin(phi)] [ cos(phi), -rho*sin(phi), 0] J = rho^2*sin(phi)