Examples: Parametrized surfaces
Contents
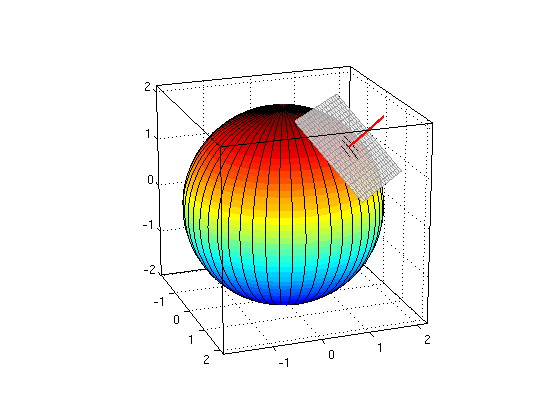
(1a) Sphere with radius 2
Consider the points (x,y,z) with x^2+y^2+z^2. Find a parametrization using spherical coordinates phi,theta and plot the surface.
For the point (x0,y0,z0) with phi=pi/4 and theta=pi/4 find the normal vector and plot the tangent plane.
syms phi theta real Pi = sym('pi'); X = 2*sin(phi)*cos(theta) % Use spherical coordinates with rho=2 Y = 2*sin(phi)*sin(theta) Z = 2*cos(phi) R = [X,Y,Z]; Rphi = diff(R,phi) % partial derivative with respect to phi Rtheta = diff(R,theta) % partial derivative with respect to theta % Now plug in phi=pi/4, theta=pi/4: R0 = subs(R,{phi,theta},{Pi/4,Pi/4}) % point on surface Rphi0 = subs(Rphi,{phi,theta},{Pi/4,Pi/4}) % first tangent vector Rtheta0 = subs(Rtheta,{phi,theta},{Pi/4,Pi/4}) % second tangent vector N = cross(Rphi0,Rtheta0) % normal vector is cross product of tangent vectors ezsurfpar(X,Y,Z,0,2*Pi,0,Pi,theta,phi); hold on % plot surface for theta in [0,2*pi], phi in [0,Pi] plane(R0,N) % plot tangent plane hold off; nice3d; view(70,20)
X = 2*cos(theta)*sin(phi) Y = 2*sin(phi)*sin(theta) Z = 2*cos(phi) Rphi = [ 2*cos(phi)*cos(theta), 2*cos(phi)*sin(theta), -2*sin(phi)] Rtheta = [ -2*sin(phi)*sin(theta), 2*cos(theta)*sin(phi), 0] R0 = [ 1, 1, 2^(1/2)] Rphi0 = [ 1, 1, -2^(1/2)] Rtheta0 = [ -1, 1, 0] N = [ 2^(1/2), 2^(1/2), 2]
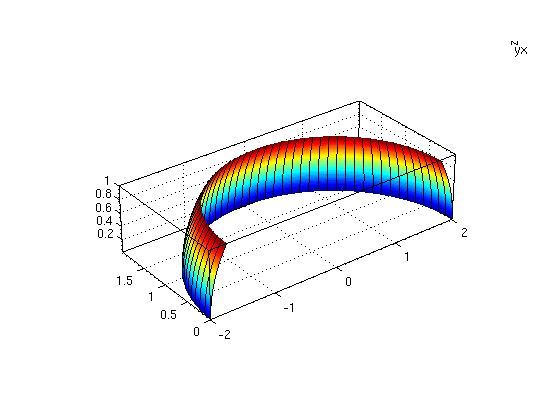
(1b) Part of sphere
Now consider the part of the sphere from (1a) with y>=0 and 0<=z<=1. Find the limits for theta and phi. Plot this surface.
Answer: y>=0 gives 0<=theta<=pi. z>=0 gives phi<=pi/2. For z=1 we have 1=z=2*cos(phi), hence cos(phi)=1/2 and phi=pi/3. Therefore the limits are 0<=theta<=pi, pi/3<=phi<=pi/2.
ezsurfpar(X,Y,Z,0,Pi,Pi/3,Pi/2,theta,phi) % plot surface for theta in [0,pi], phi in [Pi/3,Pi/2]
nice3d
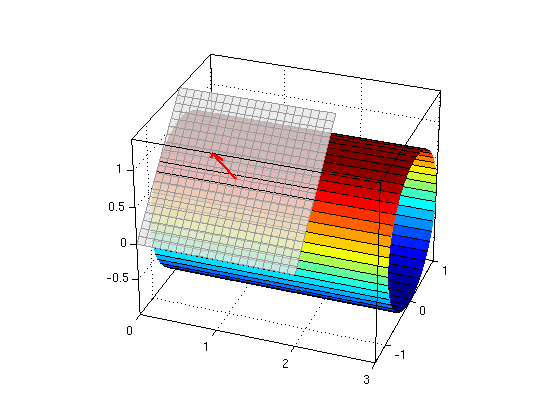
(2a) Cylinder
Consider the points (x,y,z) with y^2+z^2=1 and 0<=x<=3. Find a parameterization and plot the surface.
For the point (x0,y0,z0)=(1,-1/sqrt(2),1/sqrt(2)) find the normal vector and plot the tangent plane.
Answer: We use the parametrization (x,cos(theta),sin(theta)) with 0<=theta<=2*pi, 0<=x<=3.
syms theta x real Pi = sym('pi'); X = x; Y = cos(theta); Z = sin(theta) % parametrization of surface R = [X,Y,Z]; Rtheta = diff(R,theta) % partial derivative w.r.t. theta Rx = diff(R,x) % partial derivative w.r.t. x x0 = 1; theta0 = 3/4*Pi; % parameters for (x0,y0,z0), plug this in for R, Rtheta, Rx: R0 = subs(R,{theta,x},{theta0,x0}) % point on surface Rtheta0 = subs(Rtheta,{theta,x},{theta0,x0}) % first tangent vector Rx0 = subs(Rx,{theta,x},{theta0,x0}) % second tangent vector N = cross(Rtheta0,Rx) % normal vector ezsurfpar(X,Y,Z,0,2*pi,0,3,theta,x); hold on % plot surface for theta in [0,2*pi], x in [0,3] plane(R0,N) % plot tangent plane hold off; nice3d; view(20,30)
Z = sin(theta) Rtheta = [ 0, -sin(theta), cos(theta)] Rx = [ 1, 0, 0] R0 = [ 1, -2^(1/2)/2, 2^(1/2)/2] Rtheta0 = [ 0, -2^(1/2)/2, -2^(1/2)/2] Rx0 = [ 1, 0, 0] N = [ 0, -2^(1/2)/2, 2^(1/2)/2]
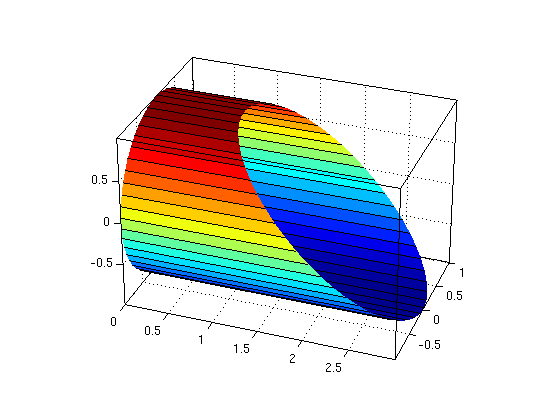
(2b) Part of cylinder
Now consider the part of the cylinder from (2a) with x>=0 and x+z<=2. Find the limits for the parameters and plot the surface.
Answer: Since x<=2-z and z=sin(theta) we get 0<=theta<=2*pi, 0<=x<=2-sin(theta).
ezsurfpar(X,Y,Z,0,2*pi,0,2-sin(theta),theta,x) % plot surface for theta in [0,2*pi], x in [0,2-sin(theta)]
nice3d; view(20,30)