Examples for vector fields and potentials
Contents
You need to download new m-files.
Download the files vectorfield.m, vectorfield3.m, ezisosurf.m, ezpcolor.m, posneg.m
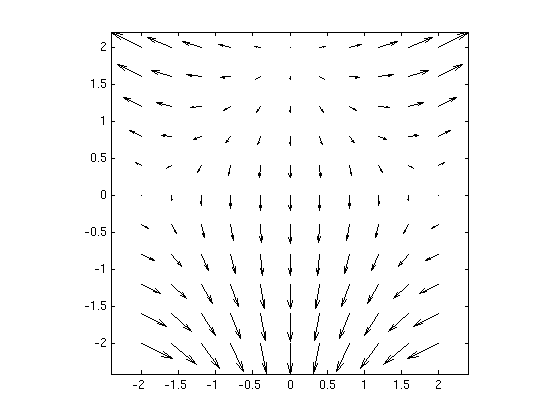
(1a) Plot a 2D vector field
Plot the 2D vector field F = ( 2*x*y , x^2+2*y-4 ) for x,y in [-2,2].
syms x y real F = [ 2*x*y , x^2+2*y-4 ]; vectorfield(F,-2:.4:2,-2:.4:2)
(1b) Find a potential f(x,y) for the vector field F
For the vector field F from (1a) find a potential f(x,y). Check that grad f = F.
Plot the vector field together with the contour plot of the potential. How can you see geometrically that the potential fits to the given vector field?
Answer: We can see that F is the gradient of f: The vector field is orthogonal on the contour curves, and the vectors point towards higher values of f.
f = potential(F,[x y]) % find potential with respect to variables (x,y) simplify(jacobian(f,[x y]) - F) % gives zero % We use jacobian(f,[x y]) to compute gradient, since this gives row vector. % Using gradient(f,[x y]) gives a column vector. vectorfield(F,-2:.4:2,-2:.4:2); hold on ezcontourc(f,[-2 2 -2 2],30); colorbar; hold off title('Vector field F with contours of potential f')
f = y*x^2 + y*(y - 4) ans = [ 0, 0]

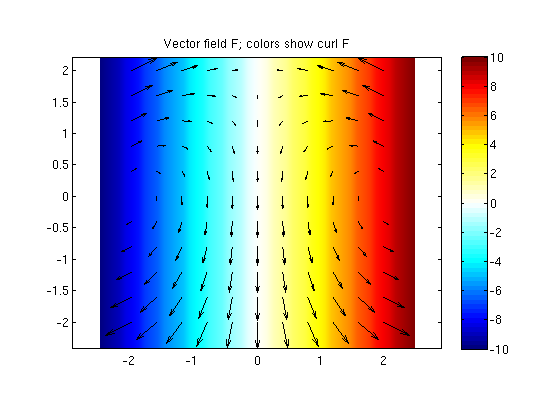
(2) Try to find a potential for vector field F = ( -2*x*y , x^2+2*y-4 ).
First find the curl of the vector field. How do the values of curl F correspond geometrically to the vector field?
Answer: We find that curl F = (0,0,4*x) is nonzero, hence the potential does not exist.
We see that the curl is positive for x>0 and negative for x<0. Imagine that the arrows describe a fluid flow. Then an object held at a position with positive x will be rotated counterclockwise. An object held at a position with negative x will be rotated clockwise.
syms x y z F = [ -2*x*y , x^2+2*y-4 ]; f = potential(F,[x y]) % Matlab returns "NaN" which means there is no answer G = curl([F,0],[x y z]) % check the curl: use [F,0] since we need vector of 3 components vectorfield(F,-2:.4:2,-2:.4:2); hold on ezpcolor(G(3),[-2.5 2.5 -2.5 2.5]); colorbar; hold off colormap(posneg) title('Vector field F; colors show curl F')
f = NaN G = 0 0 4*x
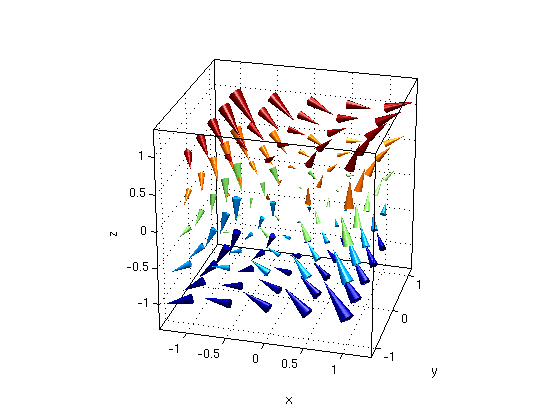
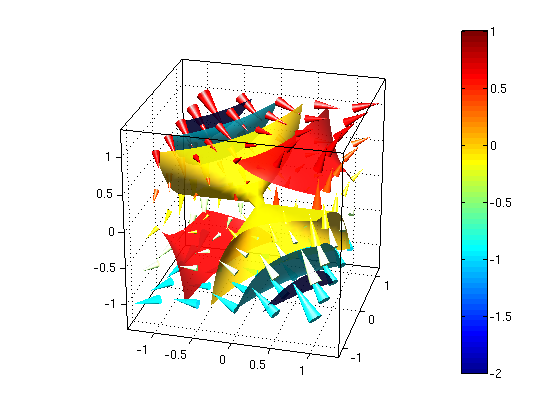
(3) Find potential for 3D vector field F
Consider the vector field F = ( y+2*z, x-z, 2*x-y ). Find curl F. Find a potential f if possible.
Plot the vector field together with the contour plot of the potential. How can you see geometrically that the potential fits to the given vector field?
Answer: We can see that F is the gradient of f: The vector field is orthogonal on the contour surfaces, and the vectors point towards higher values of f.
syms x y z real F = [ y+2*z, x-z, 2*x-y ]; G = curl(F,[x y z]) % curl F is zero f = potential(F,[x y z]) figure(1) % Plot vector field F vectorfield3(F,-1:.5:1,-1:.5:1,-1:.5:1); view(15,25) figure(2) % Plot vector field F together with contours of potential f vectorfield3(F,-1:.5:1,-1:.5:1,-1:.5:1); hold on ezisosurf(f,[-1 1 -1 1 -1 1],-2:1); % Plot contour surfaces for f=-2,-1,0,1 colorbar; alpha(0.9); hold off; view(15,25);
G = 0 0 0 f = x*(y + 2*z) - y*z