Example where curl F is zero, yet there exists no potential
Contents
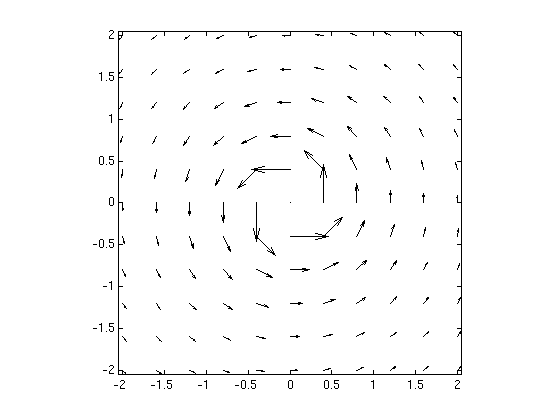
Consider the 2D vector field F = (-y,x)/(x^2+y^2)
Let D be the domain of all points (x,y) except (0,0). Consider the vector field F = (-y,x)/(x^2+y^2) on the domain D. Plot the vector field. By looking at this vector field: explain why there cannot be a potential on the domain D.
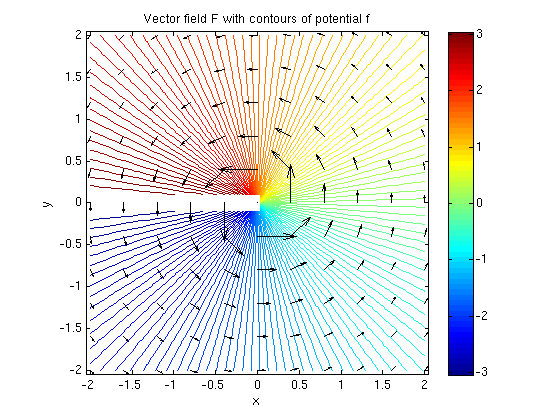
Answer: The vector field is tangential to circles. If we move around a circle in the direction of the arrows, the function f would have to keep increasing (since grad f = F). But when we arrive at the starting point we must have the same value again - this is a contradiction!
syms x y z F = [-y,x]/(x^2+y^2); vectorfield(F,-2:.4:2,-2:.4:2);
Try to find a potential for this vector field
Show that curl F is zero on D. Try to find a potential f(x,y). Is this a potential on the domain D?
Answer: We can find a potential f: It is the function which gives the angle phi for a point (x,y). In computer programs this function is called atan2(y,x) and gives angles in (-pi,pi]. Note that the function f(x,y) has a jump of 2*pi at the negative x-axis! Therefore this potential only works for domains which do not contain any part of the negative x-axis. For our domain D it is not possible to find a potential.
Note that the theorem from class only works on "box domains" or the whole space. The theorem does not work on domains with "holes".
G = simplify(curl([F,0],[x y z])) % curl F is zero! f = potential(F,[x y]) % Matlab actually finds a potential f % Matlab gives f = -atan(x/y) which is atan(y/x) up to multiple of pi f = atan2(y,x) % atan2(y,x) gives the polar angle phi for point (x,y) % this is a better answer since it works in all quadrants gradient(f,[x y]) % We see that the gradient is indeed F ezcontourc(f,[-2 2 -2 2],120); colorbar; hold on % Plot the potential vectorfield(F,-2:.4:2,-2:.4:2); hold off % Plot the vector field title('Vector field F with contours of potential f')
G = 0 0 0 f = -atan(x/y) f = atan2(y, x) ans = -y/(x^2 + y^2) x/(x^2 + y^2)