"Work integral" for vector field along a curve
Contents
- (1a) Consider the vector field F = (y,-x,-z).
- (1b) Let C1 be the curve from the point (1,0,1) to the point (0,1,-1) along the circle z=1, x^2+y^2=1. Find the work W for the curve C1.
- (1c) Let C2 be the straight line from the point (1,0,1) to the point (0,1,1). Find the work W for the curve C2.
- (2a) Consider the vector field F = (x+y,x-y,-z).
- (2b) Let C1 be the curve from the point (1,0,1) to the point (0,1,1) along the circle z=1, x^2+y^2=1. Find the work W for the curve C1.
- (2c) Let C2 be the straight line from the point (1,0,1) to the point (0,1,1). Find the work W for the curve C2.
- (2d) Find the work for any curve from (0,1,1) to (1,0,1) using the potential!
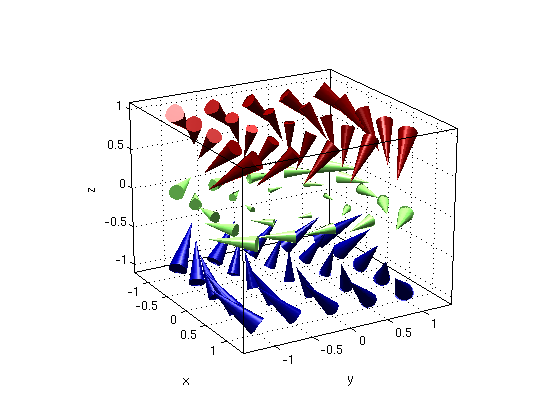
(1a) Consider the vector field F = (y,-x,-z).
Find G = curl F. Is the vector field conservative?
Answer: We have curl F = (0,0,-2). Hence the vector field is not conservative.
syms x y z F = [y,-x,-z]; % given vector field G = curl(F) % note: Matlab gives curl as column vectorfield3(F,-1:.5:1,-1:.5:1,-1:1) view(60,20)
G = 0 0 -2
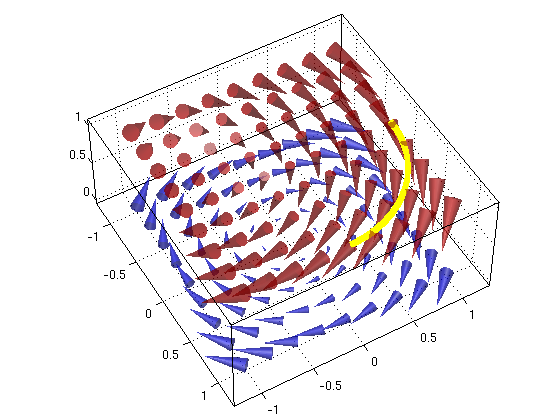
(1b) Let C1 be the curve from the point (1,0,1) to the point (0,1,-1) along the circle z=1, x^2+y^2=1. Find the work W for the curve C1.
Answer: The work is W = -pi/2 (we have to spend energy to move along this curve)
syms t real % parameter t R = [cos(t),sin(t),1]; % parametrization R(t) a = 0; b = pi/2; % interval for t FR = subs(F,{x,y,z},{R(1),R(2),R(3)}) % in F substitute parametrization R for x,y,z Rp = diff(R,t) % R'(t) W = int(dot(FR,Rp),t,a,b) % find work integral vectorfield3(F,-1:.25:1,-1:.25:1,[0 1]) % plot vector field for z=0,1 hold on; alpha(0.5) h = Ezplot3(R(1),R(2),R(3),[a,b]); % (need to use Ezplot3, fixes bugs in ezplot3) set(h,'Linewidth',10,'Color','yellow') % make curve thick, yellow hold off; view(60,50)
FR = [ sin(t), -cos(t), -1] Rp = [ -sin(t), cos(t), 0] W = -pi/2
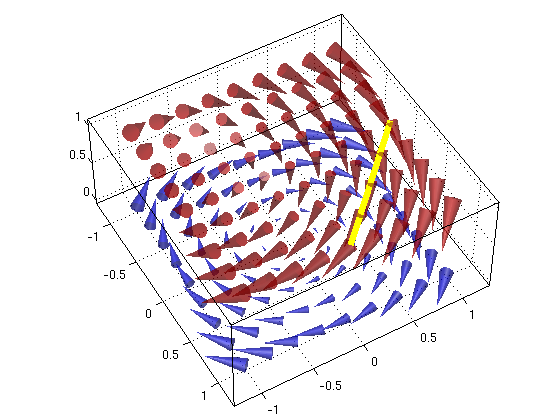
(1c) Let C2 be the straight line from the point (1,0,1) to the point (0,1,1). Find the work W for the curve C2.
Answer: Now the work is W = -1, which is different from (1b) (not surprising as the vector field is not conservative)
A = [1,0,1]; B = [0,1,1]; % endpoints R = A + t*(B-A) % parametrization of line from A to B a = 0; b = 1; % interval for t FR = subs(F,{x,y,z},{R(1),R(2),R(3)}) % in F substitute parametrization R for x,y,z Rp = diff(R,t) % R'(t) W = int(dot(FR,Rp),t,a,b) % find work integral vectorfield3(F,-1:.25:1,-1:.25:1,[0 1]) % plot vector field for z=0,1 hold on; alpha(0.5) h = Ezplot3(R(1),R(2),R(3),double([a,b])); % need to use Ezplot3 since ezplot3 has bug set(h,'Linewidth',10,'Color','yellow') % make curve thick, yellow hold off; view(60,50)
R = [ 1 - t, t, 1] FR = [ t, t - 1, -1] Rp = [ -1, 1, 0] W = -1
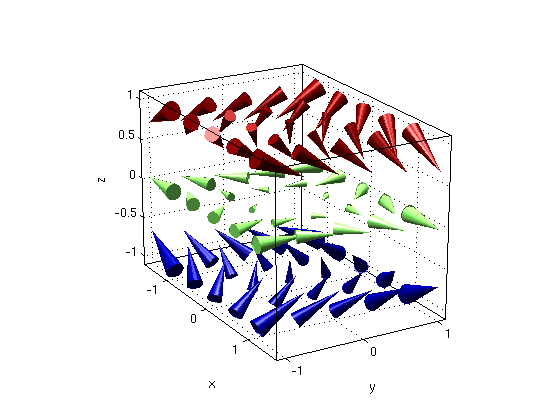
(2a) Consider the vector field F = (x+y,x-y,-z).
Find G = curl F. Is the vector field conservative?
Answer: We have curl F = (0,0,0). Hence the vector field is conservative.
syms x y z F = [x+y,x-y,-z]; % given vector field G = curl(F) % note: Matlab gives curl as column vectorfield3(F,-1:.5:1,-1:.5:1,-1:1) view(60,20)
G = 0 0 0
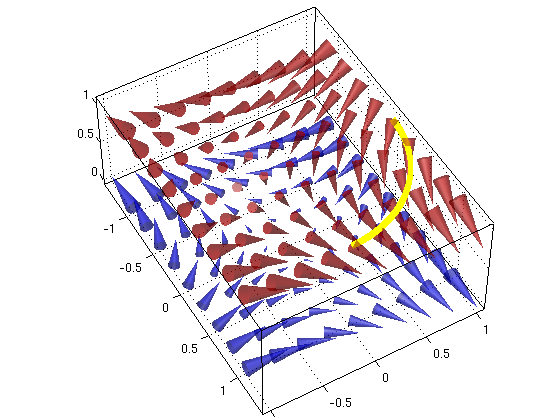
(2b) Let C1 be the curve from the point (1,0,1) to the point (0,1,1) along the circle z=1, x^2+y^2=1. Find the work W for the curve C1.
Answer: The work is W = -1 (we have to spend energy to move along this curve)
syms t real % parameter t Pi = sym('pi'); R = [cos(t),sin(t),1]; % parametrization R(t) a = 0; b = Pi/2; % interval for t FR = subs(F,{x,y,z},{R(1),R(2),R(3)}) % in F substitute parametrization R for x,y,z Rp = diff(R,t) % R'(t) W = int(dot(FR,Rp),t,a,b) % find work integral vectorfield3(F,-1:.25:1,-1:.25:1,[0 1]) % plot vector field for z=0,1 hold on; alpha(0.5) h = Ezplot3(R(1),R(2),R(3),double([a,b])); % (need to use Ezplot3, fixes bugs in ezplot3) set(h,'Linewidth',10,'Color','yellow') % make curve thick, yellow hold off; view(60,50)
FR = [ cos(t) + sin(t), cos(t) - sin(t), -1] Rp = [ -sin(t), cos(t), 0] W = -1
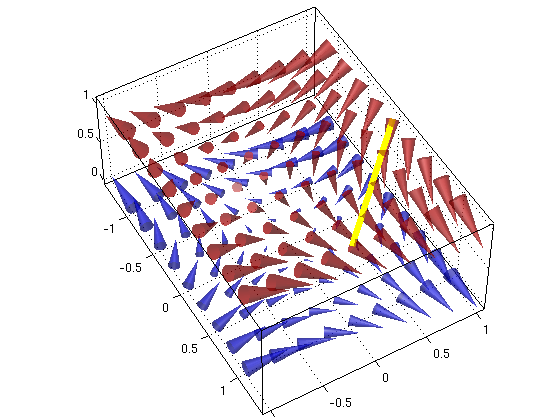
(2c) Let C2 be the straight line from the point (1,0,1) to the point (0,1,1). Find the work W for the curve C2.
Answer: Now the work is W = -1, which is the same as (2b) (since the vector field is conservatitve)
A = [1,0,1]; B = [0,1,1]; % endpoints R = A + t*(B-A) % parametrization of line from A to B a = 0; b = 1; % interval for t FR = subs(F,{x,y,z},{R(1),R(2),R(3)}) % in F substitute parametrization R for x,y,z Rp = diff(R,t) % R'(t) W = int(dot(FR,Rp),t,a,b) % find work integral vectorfield3(F,-1:.25:1,-1:.25:1,[0 1]) % plot vector field for z=0,1 hold on; alpha(0.5) h = Ezplot3(R(1),R(2),R(3),double([a,b])); % need to use Ezplot3 since ezplot3 has bug set(h,'Linewidth',10,'Color','yellow') % make curve thick, yellow hold off; view(60,50)
R = [ 1 - t, t, 1] FR = [ 1, 1 - 2*t, -1] Rp = [ -1, 1, 0] W = -1
(2d) Find the work for any curve from (0,1,1) to (1,0,1) using the potential!
f = potential(F,[x y z]) % find the potential W = subs(f,{x,y,z},{0,1,1}) - subs(f,{x,y,z},{1,0,1}) % f at end point minus f at initial point
f = (x*(x + 2*y))/2 - y^2/2 - z^2/2 W = -1