Examples Wednesday, Febr. 5
Contents
(a) Plane through three given points
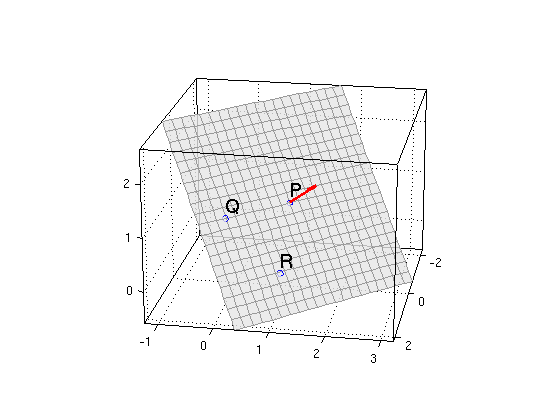
Consider the plane given by the three points P=(0,1,1), Q=(1,0,1), R=(1,1,0). Find the normal vector N and plot the plane.
P = [0,1,1]; Q = [1,0,1]; R = [1,1,0]; N = cross(Q-P,R-P) plotpts([P;Q;R],'o'); hold on texts(P,'P'); texts(Q,'Q'); texts(R,'R') plane(P,N,2,2); % 2,2 specifies width and height of rectangle hold off; nice3d view(100,20); % pick nice angle to look at plot
N =
1 1 1
(b) Distance of point from plane
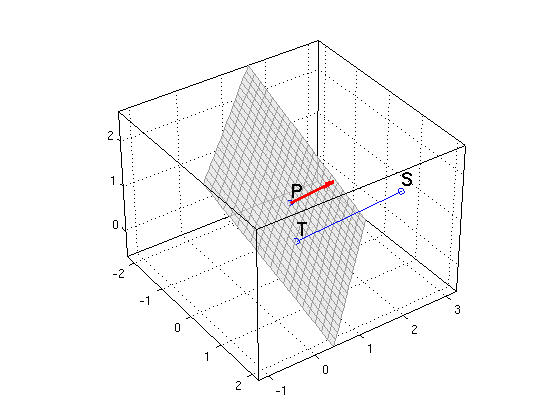
Consider the point S = (2,2,2). Find the closest point T on the plane from (a), and find the distance from S to T.
S = [2,2,2]; a = S-P % vector from P to S apar = dot(a,N)/dot(N,N)*N % projection of a onto N T = S-apar distance1 = norm(S-T) % distance using S,T distance2 = abs(dot(a,N))/norm(N) % distance using formula from class plotpts(P,'o'); hold on plotpts([S;T],'o-') % line from S to T texts(P,'P'); texts(S,'S'); texts(T,'T') plane(P,N,2,2); hold off; nice3d view(55,35) % pick nice angle to look at plot
a =
2 1 1
apar =
1.3333 1.3333 1.3333
T =
0.6667 0.6667 0.6667
distance1 =
2.3094
distance2 =
2.3094
(c) Intersection of two planes
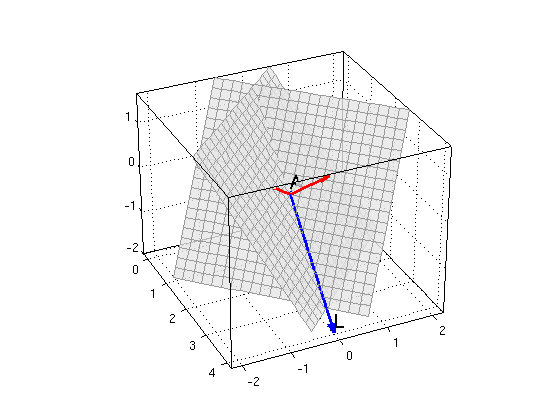
Consider the plane from (a) and the plane given by the equation x-y+z=2. Find the intersection line of the two planes: give a point A on the line and the direction vector L.
D = dot(P,N); % D-value of first plane Np = [1,-1,1]; % normal vector of second plane Dp = 2; % D-value of second plane L = cross(N,Np) % direction vector of line % find pt A which is on both planes: a = [N;Np]\[D;Dp]; % find [a1;a2;a3] such that [N;Np]*[a1;a2;a3] = [D;Dp] A = a' % write as row vector plotpts(A,'o'); texts(A,'A'); hold on plane(A,N,2,2); % plot first plane plane(A,Np,2,2) % plot second plane arrow3(A,L) % plot direction vector texts(A+L,'L') hold off; nice3d; view(65,30) % pick nice angle to look at plot
L =
2 0 -2
A =
2.0000 0 0