Examples Friday, February 7
Contents
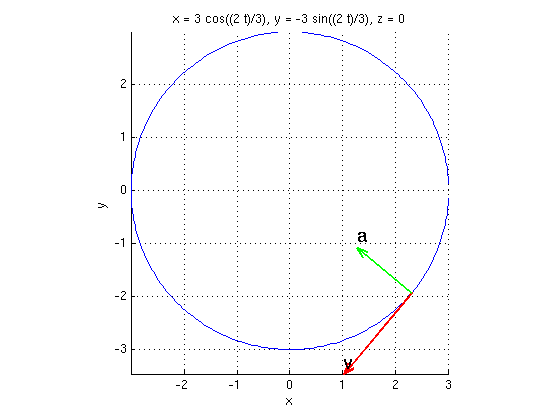
Moving around a circle with constant speed
We move with speed V=2 around a circle of radius R=3 in clockwise direction, starting at point (3,0,0). Find the position function r(t), the velocity function v(t), the acceleration function a(t). Find the period T for one full circle. Plot the resulting curve together with the velocity and acceleration vectors for t=pi/3.
syms t real % declare t as real symbolic value Pi = sym('pi'); % symbolic value pi R = sym(3); V = sym(2); b = -V/R; % need "-" for clockwise r = R*[cos(b*t),sin(b*t),0] v = diff(r,t) % differentiate with respect to t a = diff(v,t) T = 2*Pi/abs(b) % period T for one full circle ezplot3(r(1),r(2),r(3),[0,double(T)]); hold on r0 = subs(r,t,Pi/3) % substitute t=pi/3 in r v0 = subs(v,t,Pi/3) a0 = subs(a,t,Pi/3) arrow3(r0,v0,'r'); texts(r0+v0,'v') arrow3(r0,a0,'g'); texts(r0+a0,'a') hold off; axis equal; view(0,90); % look at x,y plane
r = [ 3*cos((2*t)/3), -3*sin((2*t)/3), 0] v = [ -2*sin((2*t)/3), -2*cos((2*t)/3), 0] a = [ -(4*cos((2*t)/3))/3, (4*sin((2*t)/3))/3, 0] T = 3*pi r0 = [ 3*cos((2*pi)/9), -3*sin((2*pi)/9), 0] v0 = [ -2*sin((2*pi)/9), -2*cos((2*pi)/9), 0] a0 = [ -(4*cos((2*pi)/9))/3, (4*sin((2*pi)/9))/3, 0]
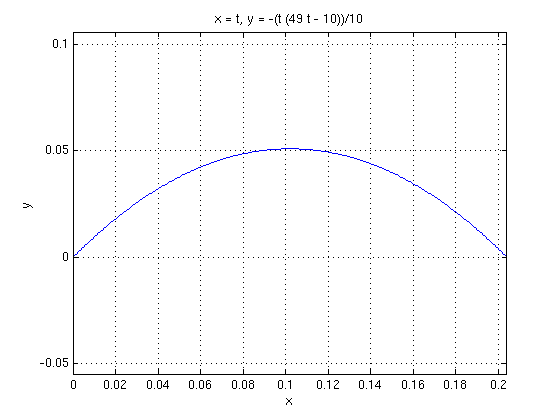
Throwing a ball
I throw a ball at time t=0 from the point (0,0) with initial velocity (1,1). Find the position function r(t). Find the time the ball hits the ground, and the distance from the starting point.
syms t real % declare t as real symbolic value g = 9.8 % acceleration from gravity r0 = [0, 0]; % initial position v0 = [1, 1]; % initial velocity a = [0, -g] % acceleration vector using Newton's law v = v0 + int(a,t,0,t) % integrate for variable t from lower bound 0 to upper bound t r = r0 + int(v,t,0,t) ts = solve(r(2),t) % find t-values where y-component is zero: ts(1)=0, ts(2)=2/g distance = subs(r(1),t,ts(2)) % substitute t=ts(2) in x-component r(1) ezplot(r(1),r(2),[0,double(ts(2))]); axis equal; grid on % plot trajectory
g =
9.8000
a =
0 -9.8000
v =
[ 1, 1 - (49*t)/5]
r =
[ t, -(t*(49*t - 10))/10]
ts =
0
10/49
distance =
10/49