Examples Monday, February 10
Contents
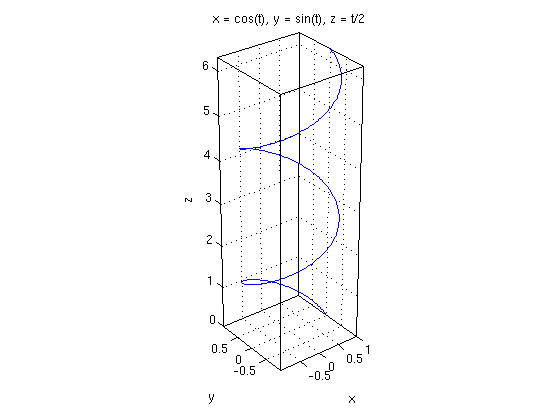
Helix
Consider the curve r(t) = (cos(t), sin(t), t/2) for t going from 0 to 4*pi. Plot the curve and find its length.
syms t real % declare t as real symbolic value Pi = sym('pi'); % symbolic pi r = [cos(t),sin(t),t/2] v = diff(r,t) % velocity V = simplify(norm(v)) % speed L = int(V,t,0,4*Pi) % length of curve for t going from 0 to 4*pi ezplot3(r(1),r(2),r(3),[0,4*pi]); nice3d
r = [ cos(t), sin(t), t/2] v = [ -sin(t), cos(t), 1/2] V = 5^(1/2)/2 L = 2*pi*5^(1/2)
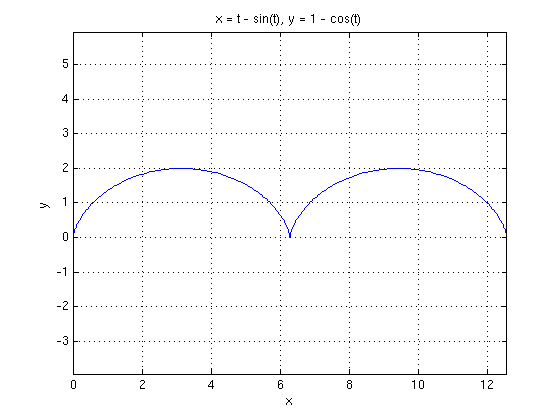
Cycloid
Consider the curve r(t) = ( t-sin(t), 1-cos(t) ). Plot the curve for t going from 0 to 4*pi. Find the length of the curve for t going from 0 to 2*pi.
syms t real % declare t as real symbolic value r = [t-sin(t),1-cos(t)]; v = diff(r,t) % velocity V = simplify(norm(v)) % speed L = int(V,t,0,2*Pi) % length of curve for t going from 0 to 2*pi ezplot(r(1),r(2),[0,4*pi]); axis equal; grid on
v = [ 1 - cos(t), sin(t)] V = 2^(1/2)*(1 - cos(t))^(1/2) L = 8