Examples Wednesday, February 12
Contents
(a) Length of curve
Consider the curve r(t) = ( t, t^2, t^3 ) for t in [0,1.5] and find its length.
syms t real % declare t as real symbolic value r = [t,t^2,t^3]; v = diff(r,t) % velocity V = simplify(norm(v)) % speed L = int(V,t,0,1.5) % integrate V for t=0 to 1.5 % Matlab returns int(...) since it cannot find an antiderivative L_numeric = vpa(L,7) % use numerical integration to obtain 7-digit accuracy
v = [ 1, 2*t, 3*t^2] V = (9*t^4 + 4*t^2 + 1)^(1/2) L = int((9*t^4 + 4*t^2 + 1)^(1/2), t == 0..3/2) L_numeric = 4.597919
(b) Decomposition of the acceleration vector, change in speed V', curvature kappa
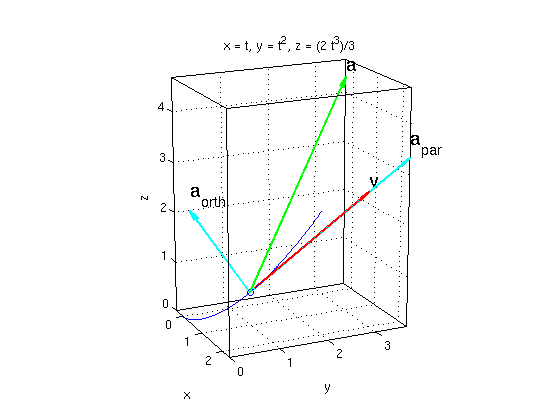
Consider the curve r(t) = ( t, t^2, (2/3)*t^3 ). Plot this curve for t in [0,1.5].
For t=1 plot the velocity vector v and the acceleration vector a.
Find the decomposition a = a_par + a_orth where a_par is parallel to v, a_orth is orthogonal on v. Use this to find the change of speed V' and the curvature kappa for this point.
r = [t,t^2,2/3*t^3]; v = diff(r,t) % velocity a = diff(v,t) % acceleration r0 = subs(r,t,1); % substitute t=1 v0 = subs(v,t,1) a0 = subs(a,t,1) V0 = norm(v0) % speed a_par = dot(a0,v0)/dot(v0,v0)*v0 % acceleration component parallel to curve a_orth = a0 - a_par % acceleration component orthogonal to curve kappa = norm(a_orth)/V0^2 % curvature Vprime = dot(a0,v0)/V0 % change of speed ezplot3(r(1),r(2),r(3),[0,1.5]); hold on plotpts(r0,'o') arrow3(r0,v0,'r'); texts(r0+v0,'v') arrow3(r0,a0,'g'); texts(r0+a0,'a') arrow3(r0,a_par,'c'); texts(r0+a_par,'a_{par}') arrow3(r0,a_orth,'c'); texts(r0+a_orth,'a_{orth}') hold off; nice3d view(65,17) % pick nice angle to look at plot
v = [ 1, 2*t, 2*t^2] a = [ 0, 2, 4*t] v0 = [ 1, 2, 2] a0 = [ 0, 2, 4] V0 = 3 a_par = [ 4/3, 8/3, 8/3] a_orth = [ -4/3, -2/3, 4/3] kappa = 2/9 Vprime = 4
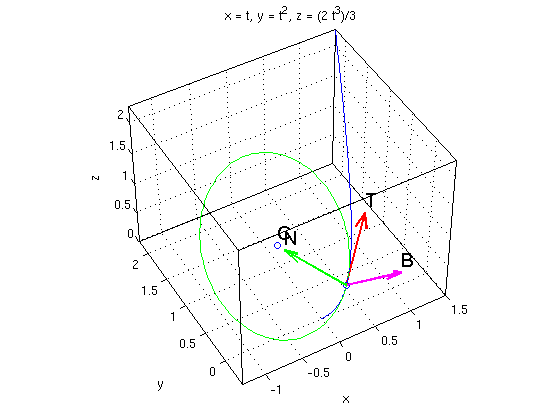
(c) Tangent vector T, normal vector N, binormal vector B, osculating circle
For the curve from (b) consider now the point with t=1/2. Find the unit tangent vector T, the normal vector N and the binormal vector B. Plot the curve with the vectors T, N,B and the osculating circle.
r0 = subs(r,t,1/2); % substitute t=1/2 now v0 = subs(v,t,1/2) a0 = subs(a,t,1/2) V0 = norm(v0) % speed a_par = dot(a0,v0)/dot(v0,v0)*v0 % acceleration component parallel to curve a_orth = a0 - a_par % acceleration component orthogonal to curve kappa = norm(a_orth)/V0^2 % curvature T = v0/V0 % unit tangent vector N = a_orth/norm(a_orth) % normal vector B = cross(T,N) % binormal vector R = 1/kappa % radius of osculating circle = 1/curvature C = r0 + R*N % center of osculating circle ezplot3(r(1),r(2),r(3),[0,1.5]); hold on plotpts(r0,'o') arrow3(r0,T,'r'); texts(r0+T,'T') arrow3(r0,N,'g'); texts(r0+N,'N') arrow3(r0,B,'m'); texts(r0+B,'B') plotpts(C,'o'); texts(C,'C') circle3(C,B,R,'g') % osculating circle hold off; nice3d view(-30,45) % pick nice angle to look at plot
v0 = [ 1, 1, 1/2] a0 = [ 0, 2, 2] V0 = 3/2 a_par = [ 4/3, 4/3, 2/3] a_orth = [ -4/3, 2/3, 4/3] kappa = 8/9 T = [ 2/3, 2/3, 1/3] N = [ -2/3, 1/3, 2/3] B = [ 1/3, -2/3, 2/3] R = 9/8 C = [ -1/4, 5/8, 5/6]