Examples Monday, February 17
Contents
Curvature of Cycloid
Find the curvature of the cycloid as a function of t. Make a plot of this function for t in [0,2*pi].
syms t real Pi = sym('pi'); r = [t-sin(t), 1-cos(t), 0]; v = diff(r,t) a = diff(v,t) kappa = simplify( norm(cross(a,v))/norm(v)^3 ) % formula with cross product ezplot(kappa,[0,2*pi]) % Plot kappa title('curvature \kappa(t)') % Note: kappa becomes infinite for t=0, 2*pi
v = [ 1 - cos(t), sin(t), 0] a = [ sin(t), cos(t), 0] kappa = 2^(1/2)/(4*(1 - cos(t))^(1/2))

Vectors T, N and osculating circle
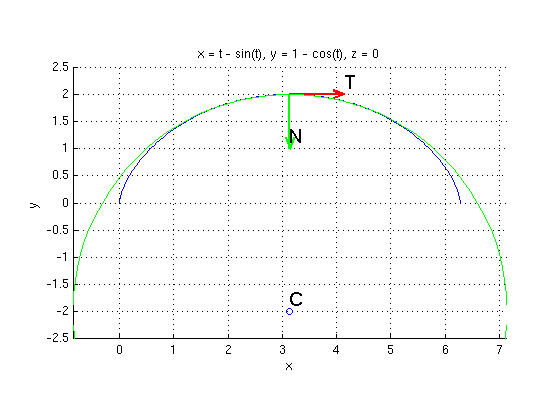
For t=pi find kappa, T, N. Plot the cycloid together with the osculating circle at t=pi.
(Try also other values like pi/2.)
t0 = Pi; % Try also t0 = Pi/2 r0 = subs(r,t,t0); % Plug in t=t0 v0 = subs(v,t,t0); a0 = subs(a,t,t0); apar = dot(a0,v0)/dot(v0,v0)*v0; % decompose a0 = apar + aorth aorth = simplify(a0 - apar); kappa0 = subs(kappa,t,t0); % curvature, same as norm(aorth)/dot(v0,v0) T = v0/norm(v0) % unit tangent vector T N = aorth/norm(aorth) % normal vector N B = cross(T,N); % binormal vector R = 1/kappa0 % radius of osculating circle C = r0 + R*N % center of osculating circle ezplot3(r(1),r(2),r(3),[0,2*pi]); hold on % plot curve for t=0...2*pi arrow3(r0,T,'r'); texts(r0+T,'T') arrow3(r0,N,'g'); texts(r0+N,'N') plotpts(C,'o'); texts(C,'C') circle3(C,B,R,'g') % plot osculating circle (green) hold off; axis equal ylim([-2.5 2.5]) % show y between -2.5, 2.5 view(0,90); % look at xy-plane
T = [ 1, 0, 0] N = [ 0, -1, 0] R = 4 C = [ pi, -2, 0]