Example: How to prepare homework problems
Contents
Problem: finding the closest point on a line
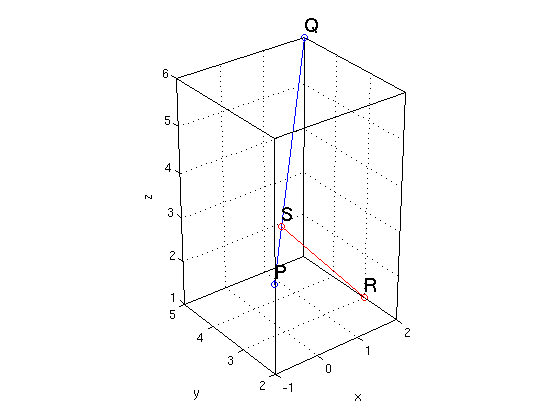
Consider the line through the points P = (-1,2,3) and Q = (2,5,6). For the point R = (2,3,1) find the closest point S on the line. Find the distance of the points R and S.
Then compute the distance of the point R to the line using the formula with the cross product. Do you get the same value?
Make a graph which shows the line and the points P,Q,R,S.
Answer:
We see that both formulas give the same value 3.5590 for the distance.
P = [-1,2,3] Q = [2,5,6] R = [2,3,1] L = Q - P % direction vector L of line a = R - P % vector from P to R b = dot(L,a)/dot(L,L)*L % projection of a onto L S = P + b % S is closest point to R distance1 = norm(R - S) % Method 1: distance of points R,S distance2 = norm(cross(L,a))/norm(L) % Method 2: formula of Thm 11.12, p. 739 plotpts([P;Q],'o-'); % plot line thru P,Q, mark pts with 'o' hold on % add to the current plot plotpts([R;S],'ro-'); % plot points R,S (connected by red line) texts(P,'P'); texts(Q,'Q'); % label points texts(R,'R'); texts(S,'S'); nice3d % when you run this in Matlab you can rotate % the graph in the figure window with the mouse hold off
P =
-1 2 3
Q =
2 5 6
R =
2 3 1
L =
3 3 3
a =
3 1 -2
b =
0.6667 0.6667 0.6667
S =
-0.3333 2.6667 3.6667
distance1 =
3.5590
distance2 =
3.5590