Plotting a Phase Portrait of an Autonomous Systems

First download the file vectfield.m .

Here we consider the following example of an autonomous system:

y₁' = 4y₁ + y₂ + y₁ y₂

y₂' = y₁ + 4 y₂ + y₂²

Plotting the vector field and trajectories

First define the right hand side function g of the differential equation as

g = inline('[4*y(1)+y(2)+y(1)*y(2) ; y(1)+4*y(2)+y(2)^2]','t','y')

Note that you must use inline('...','t','y'), despite the fact that the functions do not depend on t.

To plot the vector field for y₁ between -6 and 5 and y₂ between -6 and 1 type

vectfield(g,-6:.5:5,-6:.5:1)

a1=1; a2=-3

To plot a trajectory in the phase plane starting at a point (a1, a2) at time t=0 for increasing values of t going from 0 to 4 type

[ts,ys] = ode45(g,[0,4],[a1;a2]); 
plot(ys(:,1),ys(:,2))

To plot the trajectory in the phase plane starting at the point (a1, a2) at time t=0 for decreasing values of t going from 0 to -4 type

[ts,ys] = ode45(g,[0,-4],[a1;a2]); 
plot(ys(:,1),ys(:,2))

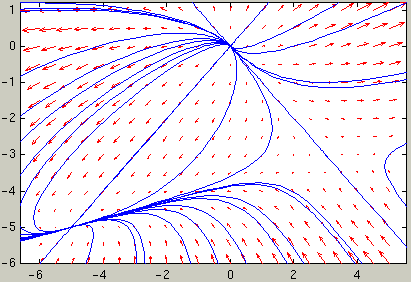
To get an idea of the behavior of the ODE, we plot the direction field and several trajectories together: We can choose e.g. the 35 starting points (a1, a2) with a1=-7,-5,-3,-1,1,3,5 and a2=-7,-5,-3,-1,1. From each of those points we plot the trajectory for t going from 0 to 4 and for t going from 0 to -4:

vectfield(g,-6:.5:5,-6:.5:1)
hold on 
for a1=-7:2:5   
  for a2=-7:2:1     
    [ts,ys] = ode45(g,[0,4],[a1;a2]); 
    plot(ys(:,1),ys(:,2))    
    [ts,ys] = ode45(g,[0,-4],[a1;a2]); 
    plot(ys(:,1),ys(:,2)) 
  end 
end
hold off

These commands will generate a number of warning messages (since some solutions don't exist for t in the whole interval [-4,4]) which you can ignore. You can use the command

  warning('off','MATLAB:ode45:IntegrationTolNotMet')

From the picture it appears that there are three critical points: A stable node, an unstable node, and a saddle point.