Solving ODEs with the Laplace Transform in Matlab

This approach works only for

linear differential equations with constant coefficients
right-hand side functions which are sums and products of
- polynomials
- exponential functions
- sine and cosine functions
- Heaviside (step) functions
- Dirac (impulse) ``functions''
initial conditions given at t = 0

The main advantage is that we can handle right-hand side functions which are piecewise defined, and which contain Dirac impulse ``functions''.

You must first save the file myplot.m in your directory. Unfortunately, the ezplot function is buggy in some versions of Matlab. If ezplot does not work, try to use myplot instead.

Simple example

Consider the initial value problem

y'' + 3 y' + 2 y = e^-t , y(0) = 4 , y'(0) = 5

Define the necessary symbolic variables:

syms s t Y

Define the right-hand side function and find its Laplace transform:

f = exp(-t)
F = laplace(f,t,s)

Find the Laplace transform of y'(t) : Y₁ = s Y - y(0)

Y1 = s*Y - 4

Find the Laplace transform of y''(t) : Y₂ = s Y₁ - y'(0)

Y2 = s*Y1 - 5

Set the Laplace transform of the left hand side minus the right hand side to zero and solve for Y:

Sol = solve(Y2 + 3*Y1 + 2*Y - F, Y)

Find the inverse Laplace transform of the solution:

sol = ilaplace(Sol,s,t)

Example with piecewise defined right-hand side function

Consider the initial value problem

y'' + 3 y' + 2 y = f(t) , y(0) = 2 , y'(0) = 3

with the right-hand side function

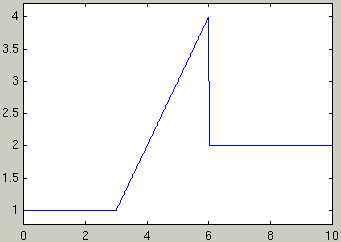
f(t) = 1 for t<3
f(t) = t -2 for 3<t<6
f(t) = 2 for t>6

Define the necessary symbolic variables:

syms s t Y

As the right-hand side function is piecewise defined, rewrite it in terms of the Heaviside function H(t) (a.k.a. unit step function):
For

f(t) = f₁(t) for t<t₁
f(t) = f₂(t) for t₁<t<t₂
f(t) = f₃(t) for t>t₂

we can write the function as

f(t) = f₁(t) + (f₂(t)-f₁(t))H(t-t₁) + (f₃(t)-f₂(t))H(t-t₂)

where H(t) denotes the Heaviside function defined by H(t) = 0 for t≤0 and H(t) = 1 for t>0.
(Note that H(t-c) = u_c(t) with u_c(t) as defined in class and the textbook).

Therefore we use in Matlab

f = 1 + ((t-2)-1)*heaviside(t-3) + (2-(t-2))*heaviside(t-6)
ezplot(f,[0,10])

Find the Laplace transform of the right hand side function f(t):

F = laplace(f,t,s)

Find the Laplace transform of y'(t) : Y₁ = s Y - y(0)

Y1 = s*Y - 2

Find the Laplace transform of y''(t) : Y₂ = s Y₁ - y'(0)

Y2 = s*Y1 - 3

Set the Laplace transform of the left hand side minus the right hand side to zero and solve for Y:

Sol = solve(Y2 + 3*Y1 + 2*Y - F, Y)

Find the inverse Laplace transform of the solution:

sol = ilaplace(Sol,s,t)

Plot the solution: (use myplot if ezplot does not work)

ezplot(sol,[0,10])

Example with Dirac ``function''

Consider the initial value problem

y'' + 2 y' + 10 y = 1 + 5 (t-5) , y(0) = 1 , y'(0) = 2

Define the necessary symbolic variables:

syms s t Y

Define the right hand side function:

f = 1 + 5*dirac(t-5)

Find the Laplace transform of the right hand side function:

F = laplace(f,t,s)

Find the Laplace transform of y'(t) : Y₁ = s Y - y(0)

Y1 = s*Y - 1

Find the Laplace transform of y''(t) : Y₂ = s Y₁ - y'(0)

Y2 = s*Y1 - 2

Set the Laplace transform of the left hand side minus the right hand side to zero and solve for Y:

Sol = solve(Y2 + 2*Y1 + 10*Y - F, Y)

Find the inverse Laplace transform of the solution:

sol = ilaplace(Sol,s,t)

Plot the solution: (use myplot if ezplot does not work)

ezplot(sol,[0,10])