dirfield(f,-2:0.2:2,-2:0.2:2)
I have updated the Matlab examples on this page for the new (MuPAD) version of the symbolic toolbox.
The book "Differential Equations with Matlab" still uses the old (Maple) version of the Symbolic Toolbox. Many of the examples give different output; some don't work at all with the new (MuPAD) version.
For many simple inputs both versions give equivalent results. But there are various differences. In particular, there are many differential equations which the old (Maple) version could solve, but which the new (MuPAD) verson cannot solve.
If you want to use a function several times it is convenient to define it as a so-called inline function:
f1 = inline('sin(x)*x','x')
defines the function f1(x)=sin(x)*x. Note that the arguments
of inline must be strings (not symbolic expressions).
You can then use the function f1 in expressions you type in.
You can also define inline functions of several variables:
g1 = inline('x*y+sin(x)','x','y')
defines the function g1(x,y)=x*y+sin(x) of two variables.
First download the file dirfield.m and put it in
the same directory as your other m-files for the homework.
Define an inline function f
of two variables t, y corresponding to the right
hand side of the differential equation y'(t) =
f(t,y(t)). E.g., for the differential
equation y'(t) = t y2
define
f = inline('t*y^2','t','y')
You have to use
inline(...,'t','y'), even if
t or y does not occur in your formula.
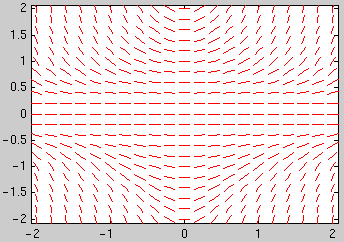
To plot the direction field for t going from t0 to t1 with
a spacing of dt and y going from y0 to y1 with a spacing of dy use
dirfield(f,t0:dt:t1,y0:dy:y1). E.g., for
t and y between -2 and 2 with a spacing of 0.2
type
dirfield(f,-2:0.2:2,-2:0.2:2)
First define the inline function
g corresponding to the
right hand side of the differential equation y'(t) =
f(t,y(t)). E.g., for the differential
equation y'(t) = t y2
define
f = inline('t*y^2','t','y')
To plot the numerical solution of an initial value
problem: For the initial condition y(t0)=y0 you can plot the
solution for t going from t0 to t1 using
ode45(f,[t0,t1],y0).
Example: To plot the solution of the initial value problem y'(t) = t y2, y(-2)=1 in the interval [-2,2] use
[ts,ys] = ode45(f,[-2,2],1)
plot(ts,ys,'o-')
The circles mark the values which were actually computed (the points are
chosen by Matlab to optimize accuracy and efficiency). The vectors
ts and ys contain the coordinates of these points, to see them
as a table type [ts,ys]
You can plot
the solution without the circles using plot(ts,ys).
To combine plots of the direction field and several
solution curves use the commands hold
on and hold off: After obtaining
the first plot type hold on, then all subsequent commands plot in
the same window. After the last plot command type hold off.
Example: Plot the direction field and the 13 solution curves with the initial conditions y(-2) = -0.4, -0.2, ..., 1.8, 2:
dirfield(f,-2:0.2:2,-2:0.2:2) hold on for y0=-0.4:0.2:2 [ts,ys] = ode45(f,[-2,2],y0); plot(ts,ys) end hold off
To obtain numerical values of the solution at
certain t values: You can specify a vector tv of t
values and use [ts,ys] = ode45(g,tv,y0). The
first element of the vector tv is the initial t value; the vector
tv must have at least 3 elements. E.g., to obtain the solution
with the initial condition y(-2)=1 at t = -2, -1.5, ..., 1.5, 2 and
display the results as a table with two columns, use
[ts,ys]=ode45(f,-2:0.5:2,1);
[ts,ys]
To obtain the numerical value of the solution at the final
t-value use
ys(end)
.
sol = dsolve('Dy=t*y^2','t')
The last argument 't' is the name of the independent variable.
Do not type y(t) instead of y.
If Matlab can't find a solution it will return an empty symbol. If Matlab finds several solutions it returns a vector of solutions.
Here there are two solutions and Matlab returns a vectorsol with two components:
sol(1) is 0 and sol(2) is -1/(t^2/2 + C3)
with an arbitrary constant C3.
The solution will contain a constant C3 (or C4,C5 etc.). You can substitute
values for the constant using
subs(sol,'C3',value). E.g., to set
C3 in sol(2) to 5 use
subs(sol(2),'C3',5)
To solve an initial value problem additionally specify an initial condition:
sol = dsolve('Dy=t*y^2','y(-2)=1','t')
To plot the solution use
ezplot(sol,[t0,t1]). Here is an example for
plotting the solution curve with the initial conditions y(-2) =
-0.4:
sol = dsolve('Dy=t*y^2','y(-2)=-0.4','t')
ezplot( sol , [-2 2])
To obtain numerical values at one or
more t values use subs(sol,'t',tval) and
double (or vpa for
more digits):
sol = dsolve('Dy=t*y^2','y(-2)=1','t')
This gives a numerical value of the solution at t=0.5:
double( subs(sol,'t',0.5) )
This computes numerical values of the solution at t=-2, -1.5, ..., 2 and displays the result as a table with two columns:
tval = (-2:0.5:2)'; % column vector with t-values
yval = double( subs(sol,'t',tval) )% column vector with y-values
[tval,yval] % display 2 columns together