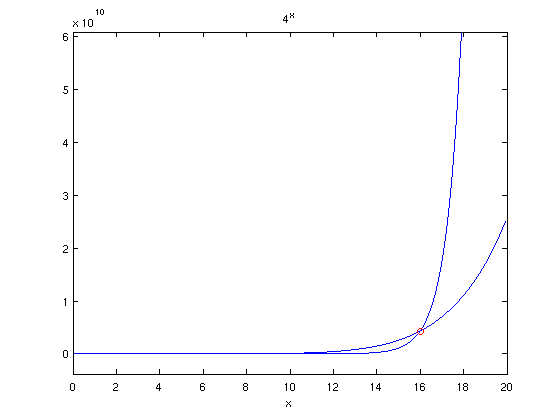
We first look at the graphs in the interval [-5,5]:
ezplot('x^8',[-5,5]); hold on ezplot('4^x',[-5,5]); hold off
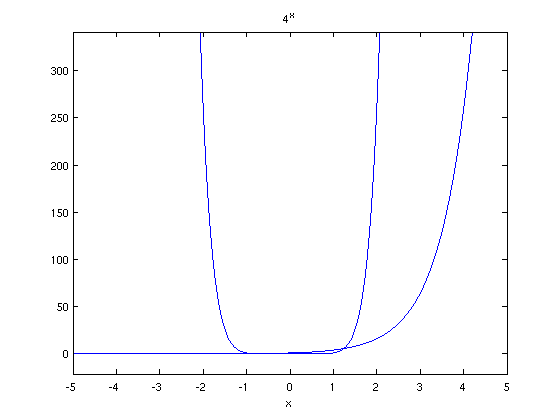
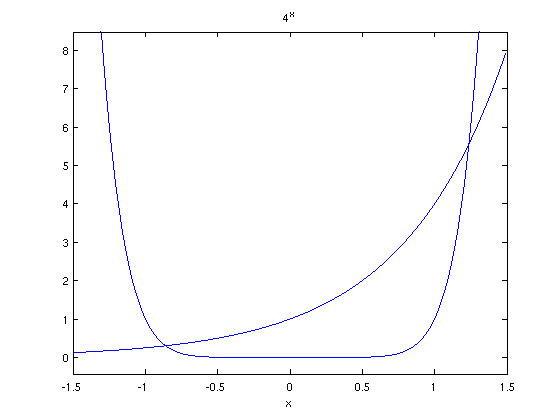
There seem to be two intersection points, near -.8 and near 1.2
ezplot('x^8',[-1.5,1.5]); hold on ezplot('4^x',[-1.5,1.5]); hold off
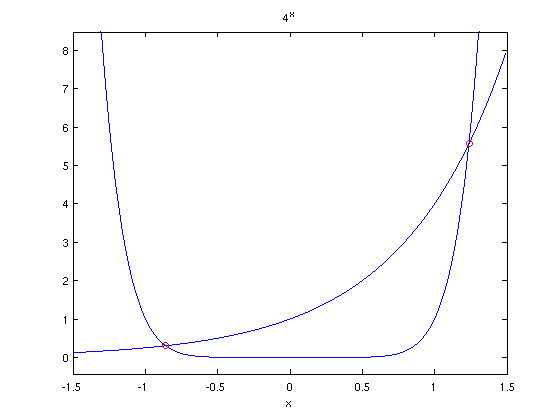
We use fzero with the difference of the two functions:
format long g % show all digits of results x1 = fzero('x^8-4^x',-.8) % find solution near -.8 x2 = fzero('x^8-4^x',1.2) % find solution near 1.2 ezplot('x^8',[-1.5,1.5]); hold on ezplot('4^x',[-1.5,1.5]); plot(x1,x1^8,'ro',x2,x2^8,'ro'); % mark intersection points with red "o" hold off
x1 =
-0.861345332309651
x2 =
1.23962772952276
solve returns a vector with all solutions in symbolic form (in terms of some strange lambertw function). Using double(s) shows the numerical value. The solve command finds 3 real solutions and 6 complex solutions
s = solve('x^8-4^x')
double(s)
s =
-8*lambertw(-1/8*log(4))/log(4)
-8*lambertw(-1,-1/8*log(4))/log(4)
-8*lambertw(-1/8*log(4)*(1/2*2^(1/2)+1/2*i*2^(1/2)))/log(4)
-8*lambertw(-1/8*i*log(4))/log(4)
-8*lambertw(-1/8*log(4)*(-1/2*2^(1/2)+1/2*i*2^(1/2)))/log(4)
-8*lambertw(1/8*log(4))/log(4)
-8*lambertw(-1/8*log(4)*(-1/2*2^(1/2)-1/2*i*2^(1/2)))/log(4)
-8*lambertw(1/8*i*log(4))/log(4)
-8*lambertw(-1/8*log(4)*(1/2*2^(1/2)-1/2*i*2^(1/2)))/log(4)
ans =
1.23962772952276
16
0.658800146101921 + 0.906903047281191i
-0.160887495730304 + 0.959104746280179i
-0.686076832044616 + 0.563629099125514i
-0.861345332309651
-0.686076832044616 - 0.563629099125514i
-0.160887495730304 - 0.959104746280179i
0.658800146101921 - 0.906903047281191i
It seems that we missed the intersection point at x=16 before. We draw the graphs again on a larger interval. Then we use fzero to find a solution near x=15
ezplot('x^8',[0,20]); hold on ezplot('4^x',[-0,20]); x3 = fzero('x^8-4^x',15) % find solution near 15 plot(x3,x3^8,'ro') % mark intersection point with red "o"
x3 =
16