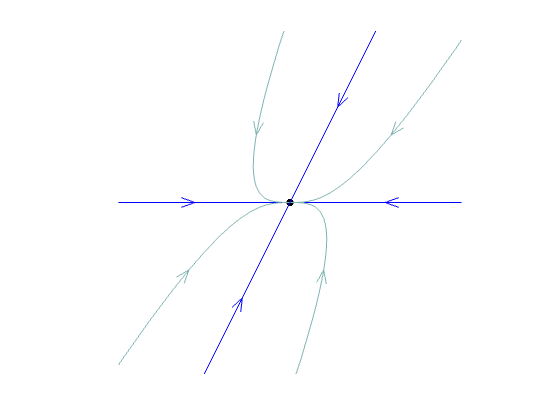
nodal sink
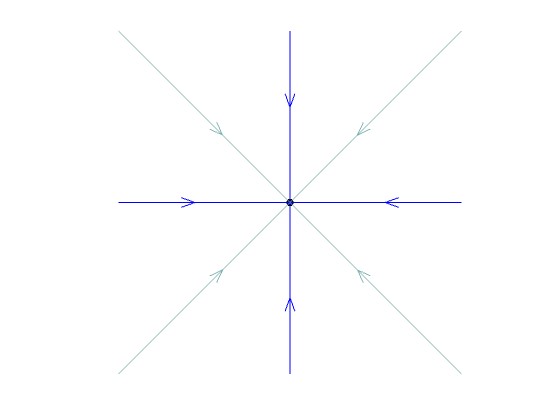
radial sink

twist sink (ccw)

spiral sink (cw)
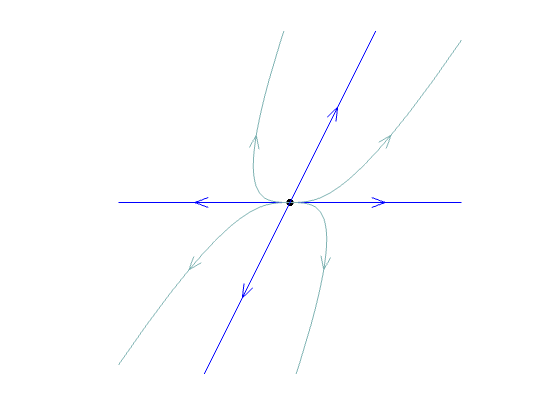
nodal source
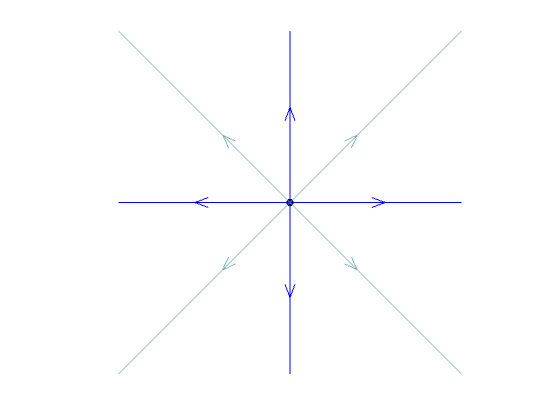
radial source

twist source (cw)

spiral source (ccw)
We say \( (x_*,y_*) \) is a stationary point if \( \left[ \matrix{f(x_*,y_*) \cr g(x_*,y_*)} \right] = \left[\matrix{0\cr0}\right]\), corresponding to a constant solution of the ODE.
The type and stability of the stationary point depends on the eigenvalues of the Jacobian matrix \[ A = \left[\matrix{\partial_xf(x_*,y_*) & \partial_yf(x_*,y_*) \cr \partial_xg(x_*,y_*) & \partial_y g(x_*,y_*)} \right] \]
| eigenvalues | linear ODE system | nonlinear ODE system | |||
|---|---|---|---|---|---|
| real | both pos. | different | nodal source | unstable, repelling | same |
| equal | radial source or twist source* | ||||
| both neg. | different | nodal sink | stable, attracting | ||
| equal | radial sink or twist sink* | ||||
| pos. and neg. | saddle | unstable, not repelling | |||
| nonreal | real part positive | spiral source | unstable, repelling | ||
| real part negative | spiral sink | stable, attracting | |||
| real part zero | center | stable, not attracting | ? | ||
*equal eigenvalues: If there are two eigenvectors we get a radial sink/source. If there is only one eigenvector (deficient case) we obtain a twist sink/source.
For twist sinks/sources, spiral sinks/sources and centers you should find out whether they are clockwise/counterclockwise. You can decide this by looking at the arrow at (1,0) (1st column of A), or the arrow at (0,1) (2nd column of A).
"same" means: type and stability for the nonlinear system are the same as for the corresponding linear system:
Note: This page only considers the case of nonzero eigenvalues. In this case both the linear and nonlinear ODE system have an isolated stationary point.
If all eigenvalues have a negative real part we get a sink (stable, attracting).
If all eigenvalues have a positive real part we get a source (unstable, repelling).
 nodal sink |
 radial sink |
 twist sink (ccw) |
 spiral sink (cw) |
 nodal source |
 radial source |
 twist source (cw) |
 spiral source (ccw) |
Remaining cases:
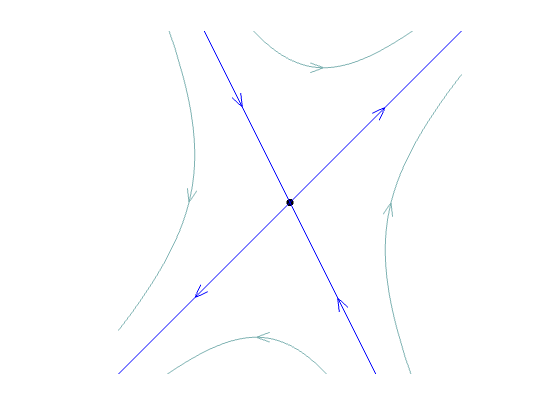 saddle (unstable, not repelling) |
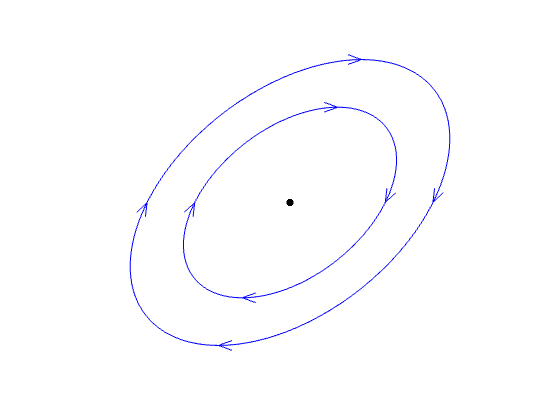 center (stable, not attracting, cw) |