Math 246 Syllabus
BD indicates sections from the textbook (Boyce &
DiPrima), M indicates sections from Differential
Equations with Matlab.
- BD 1.1-1.3: Motivation and Classification of differential equations
- BD 2.1: Linear equations
- BD 2.2: Separable equations.
Note: the separable ODE y'(t) = f(t)
g(y) has two types of solutions: Those found by
separation of variables, and constant solutions
y(t) = a where a satisfies
g(a) = 0.
- BD 2.3: Modeling with First Order Equations
- BD 2.4: Differences Between Linear and Nonlinear Equations
- BD 2.5: Population Dynamics and Related Problems
- M 5: Solution of Differential Equations
- M 6: A qualitative approach to differential equations
- BD 2.6: Exact Equations and Integrating Factors
- BD 8.1: Euler Method, Errors (backward Euler method is not done)
- BD 8.2, 8.3: Improved Euler, Runge-Kutta methods (three-term Taylor
formula is not done)
- M 7: Numerical Methods
- BD 3.1, 3.4, 3.5: Homogeneous Linear Equations with Constant
Coefficients
(reduction of order in 3.5 is skipped)
Summary of all cases is on p. 170 (bottom of page)
- BD 3.6: Nonhomogeneous Linear Equations; Method of Undetermined
Coefficients
Summary is on p. 180 (bottom of page)
- BD 3.7: Variation of Parameters
- M 10: 2nd Order Equations. Read only introduction, section ``Second
Order Equations with Matlab''.
- BD 3.2, 3.3: Fundamental Solutions and Linear Independance
- BD 3.8, 3.9: Mechanical Vibrations
- BD 6.1-6.2; M 12: Laplace Transform
- BD 7.4, 7.5, 7.6, M 13: Systems of 1st Order Linear ODEs
- BD 9.1-9.3, M 14: Nonlinear Systems and Behavior Near Critical Points
Clarification of classification of Critical Points
Table 9.3.1 on page
484 in Boyce/diPrima gives types of critical points of almost linear
systems. In the "borderline cases" actually more general types of critical points
can appear:
- r1 = r2 > 0 or
r1 = r2 < 0
- the type of the almost linear system should be more general types of N,
SpP (which can look different from the nodes and
spiral points for linear systems) . In this case the
statement below the table (that the slopes are the same as for the
linear equation) is not always true.
- r1 = i
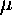 , r2 = -i
, r2 = -i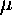 with nonzero
with nonzero 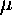
- the type of the almost linear system should be C, SpP or other.
In these cases even very near the critical point the trajectories of the
nonlinear system can be very different from those of the linear system.
Here is a correct table. One can construct examples where ``other'' types than the ones in
table 9.3.1 occur.
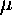 , r2 = -i
, r2 = -i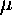 with nonzero
with nonzero 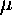
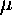 , r2 = -i
, r2 = -i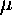 with nonzero
with nonzero