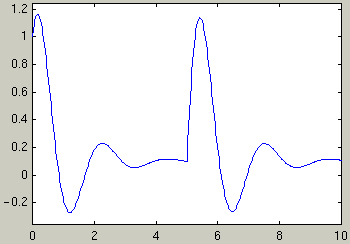
f = '1 + (t-2-1)*Heaviside(t-3) + (2-(t-2))*Heaviside(t-6)' ezplot(f,[0,10])

This approach works only for
The main advantage is that this approach allows to find symbolic solutions for right-hand side functions which are piecewise defined, and which contain Dirac impulse ``functions''.
You must first save the file Heaviside.m in
your home directory. (This fixes a bug in Matlab.)
Consider the initial value problem
y'' + 3 y' + 2 y = f(t) , y(0) = 2 , y'(0) = 3
with the right-hand side function
f(t) = 1 for t<0
f(t) = t -2 for 3<t<6
f(t) = 2 for t>6
Define the necessary symbolic variables:
syms s t Y
As the right-hand side function is piecewise defined, rewrite it in terms of the Heaviside function:
f = '1 + (t-2-1)*Heaviside(t-3) + (2-(t-2))*Heaviside(t-6)' ezplot(f,[0,10])
Find the Laplace transform of the right hand side function f(t):
F = laplace(f,t,s)
Find the Laplace transform of y'(t) : Y1 = s Y - y(0)
Y1 = s*Y - 2
Find the Laplace transform of y''(t) : Y2 = s Y1 - y'(0)
Y2 = s*Y1 - 3
Set the Laplace transform of the left hand side minus the right hand side to zero and solve for Y:
Sol = solve(Y2+3*Y1+2*Y-F,Y)
Find the inverse Laplace transform of the solution:
sol = ilaplace(Sol,s,t)
Plot the solution:
ezplot(sol,[0,10])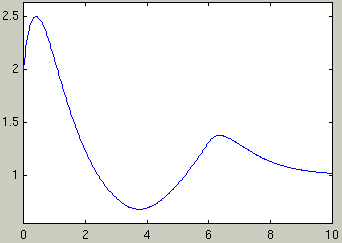
Consider the initial value problem
y'' + 2 y' + 10 y = 1 + 5
(t-5) , y(0) = 1 , y'(0) = 2
Define the necessary symbolic variables:
syms s t Y
Define the right hand side function:
f = '1 + 5*Dirac(t-5)'
Find the Laplace transform of the right hand side function:
F = laplace(f,t,s)
Find the Laplace transform of y'(t) : Y1 = s Y - y(0)
Y1 = s*Y - 1
Find the Laplace transform of y''(t) : Y2 = s Y1 - y'(0)
Y2 = s*Y1 - 2
Set the Laplace transform of the left hand side minus the right hand side to zero and solve for Y:
Sol = solve(Y2+2*Y1+10*Y-F,Y)
Find the inverse Laplace transform of the solution:
sol = ilaplace(Sol,s,t)
Plot the solution:
ezplot(sol,[0,10])