Using the Newton method to approximate b^(1/n)
Contents
Example: Compute 10^(1/3)
The algorithm uses only addition, multiplication, division. This is how calculators and computers actually compute roots.
Note that the error 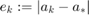 satisfies
satisfies
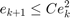
You can see below that the size of the error decreases from 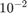 to
to 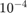 to
to 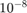 to
to 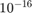 . This means that the number of correct digits double with each iteration.
. This means that the number of correct digits double with each iteration.
n = 3; digits(70) % Use vpa (variable precision arithmetic) with 70 digits b = vpa(10); exact = b^(1/n); % exact root for computing errors a = 3; % Some initial guess with a^n>b for k=1:8 a = a - (a^n-b)/(n*a^(n-1)) % Newton iteration error = double(abs(a-exact)) end
a =
2.37037037037037037037037037037037037037037037037037037037037037037037
error =
0.2159
a =
2.173508632330246913580246913580246913580246913580246913580246913580247
error =
0.0191
a =
2.154601586556418840938982225907055412855918252747313103294618350554843
error =
1.6690e-04
a =
2.154434702959438806244267854395609324195346874352286600277402465939858
error =
1.2928e-08
a =
2.154434690031883799330305534790565017460956550444977650370124977565892
error =
7.7571e-17
a =
2.154434690031883721759293566519353288224908308898563324316317120913413
error =
2.7930e-33
a =
2.154434690031883721759293566519350495259344942192108582489235506350032
error =
3.6207e-66
a =
2.154434690031883721759293566519350495259344942192108582489235506346411
error =
4.3181e-78