Example for Improved Euler method (aka RK2 method)

Contents

You need to download an m-file

You have to download the m-file dirfield.m.

function Ieuler_demo

format short g

Initial value problem

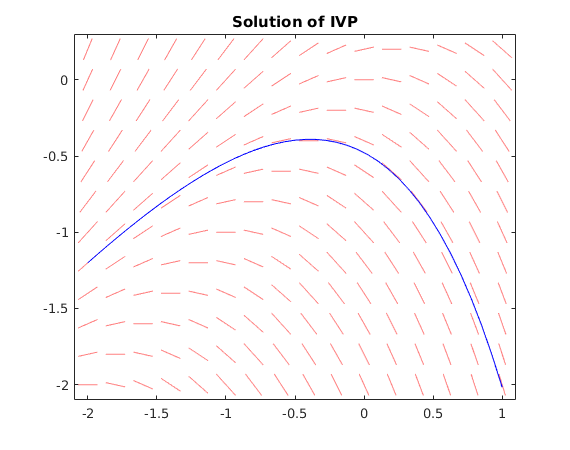
We consider the initial value problem

$$y'=y-t,\qquad y(-2)=-1.2$$

and we want to find the solution y(t) for t in [-2,1].

We use ode45 to find the solution of the initial value problem and obtain the approximation -2.01711 for y(T).

We plot the solution together with the direction field.

f = @(t,y) y-t;                   % define function f(t,y)
dirfield(f,-2:.2:1, -2:.2:0.2); hold on

t0 = -2;  y0 = -1.2;              % initial point
T = 1;                            % final t-value
[ts,ys] = ode45(f,[t0,T],y0);     % solve IVP

yfinal = ys(end);                 % value for y at time T
fprintf('y(T) = %g\n',yfinal)

plot(ts,ys,'b')                   % plot solution
title('Solution of IVP')

y(T) = -2.01711

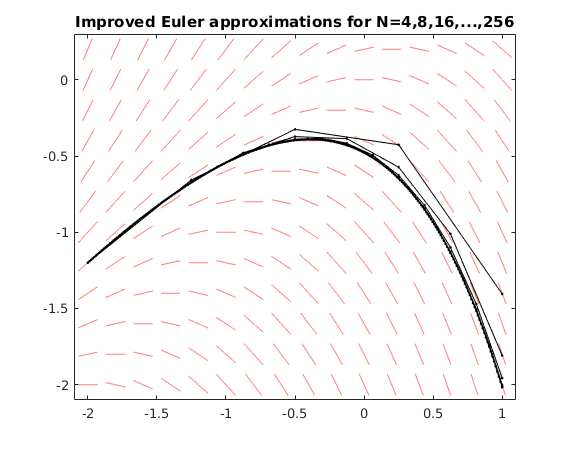
Use Improved Euler method with N=4,8,16,...,256

We see that the Improved Euler approximations get closer to the correct value y(T)=-2.01711 as N increases. Note that the errors are much smaller than the errors for the Euler method.

When we double the value of N the error gets divided by about 4. This means that the error is bounded by $C\cdot h^2$: The Improved Euler method converges with order $h^2$.

olderr = NaN;
for N = 2.^(2:8)
  [ts,ys] = IEuler(f,[t0,T],y0,N);
  err = ys(end)-yfinal;           % error
  fprintf('N = %3g, approx.for y(T) = %10g, error = %11g, quotient = %g\n',N,ys(end),err,olderr/err)
  olderr = err;
  plot(ts,ys,'k.-')               % plot Euler solution
end
hold off
title('Improved Euler approximations for N=4,8,16,...,256')

N =   4, approx.for y(T) =   -1.40474, error =    0.612376, quotient = NaN
N =   8, approx.for y(T) =   -1.80824, error =    0.208874, quotient = 2.93179
N =  16, approx.for y(T) =   -1.95615, error =   0.0609576, quotient = 3.42655
N =  32, approx.for y(T) =   -2.00068, error =   0.0164295, quotient = 3.71025
N =  64, approx.for y(T) =   -2.01285, error =   0.0042635, quotient = 3.85352
N = 128, approx.for y(T) =   -2.01602, error =  0.00108866, quotient = 3.91629
N = 256, approx.for y(T) =   -2.01683, error = 0.000278095, quotient = 3.91469

code of function IEuler(f,[t0,T],y0,N)

At each step we evaluate the slope twice: first at the current point, then at the Euler approximation. We then use the mean (s1+s2)/2 to find the new y value.

function [ts,ys] = IEuler(f,tv,y0,N);
  t0 = tv(1); T = tv(2);
  h = (T-t0)/N;                    % stepsize h
  ts = zeros(N+1,1); ys = zeros(N+1,1);
  t = t0; y = y0;                  % initial point
  ts(1) = t; ys(1) = y;

  for i=1:N
    s1 = f(t,y);                   % evaluate direction field at current point
    yE = y + s1*h;                 % find Euler value yE
    s2 = f(t+h,yE);                % evaluate direction field at Euler point
    y = y + (s1+s2)/2*h;           % use mean (s1+s2)/2 to find new y
    t = t + h;
    ts(i+1) = t; ys(i+1) = y;      % store result in vectors ts,ys
  end
end

end


Published with MATLAB® R2017a