Example for using ode45 and fzero

Contents

We drop a ball from a height of 5 feet. When does it hit the floor?

Let y(t) be the height at time t. We have y(0)=5, y'(0)=0.

Newton's law: m*y''(t) = sum of all forces:

differential equation: y'' = -32 + .01*(y')^2

function ballex

Solve initial value problem with ode45

We rewrite this as ODE system

y1' = y2, y2' = -32 + .01*y2^2

y1(0) = 5, y2(0) = 0

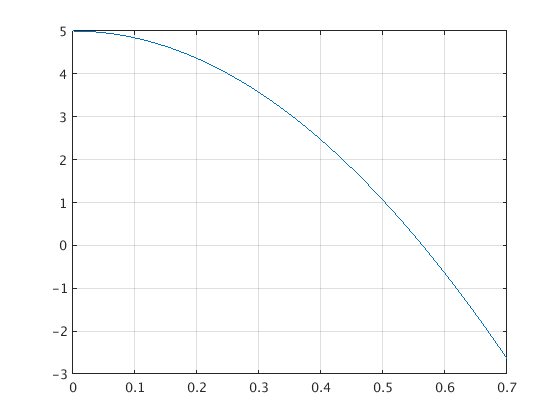
We solve this with ode45 and plot the function y(t). We see that y(t) becomes zero somewhere between 0.5 and 0.6.

f = @(t,y) [ y(2); -32 + .01*y(2)^2 ];  % define function f(t,y)
[ts,ys] = ode45(f,[0,0.7],[5;0]);        % solve ODE for t=0...0.7
                  % ys(:,1) are values for y(t), ys(:,2) are values for y'(t)
plot(ts,ys(:,1)); grid on

Write a function b=yval(T) which finds y(T)

Then we use this to find yval(.5), yval(.55), yval(.6).

We see that y(t) becomes zero near t=0.55

function b = yval(T)
  f = @(t,y) [ y(2); -32 + .01*y(2)^2 ];  % define function f(t,y)
  [ts,ys] = ode45(f,[0,T],[5;0]);         % solve ODE for t=0...T
  b = ys(end,1);                          % return final value for y(t)
                                          % last row of ys, 1st column
end

yval(.5)
yval(.55)
yval(.6)

ans =
    1.0522
ans =
    0.2361
ans =
   -0.6527

Use fzero to find zero of yval(T)

We know that yval(0)=5>0 and yval(1)<0. So we use fzero to find a root in the interval [0,1].

Actually, yval(T) only works with T different from zero, so we use [1e-5,1].

We can use optimset to show each iteration. We see that fzero called the function yval 11 times.

ts = fzero(@yval,[1e-5,1])

opt = optimset('Display','iter'); % show iterations
ts = fzero(@yval,[1e-5,1],opt)

ts =
    0.5637
 
 Func-count    x          f(x)             Procedure
    2           1e-05             5        initial
    3        0.328671       3.28147        interpolation
    4        0.328671       3.28147        interpolation
    5        0.516968      0.783503        interpolation
    6        0.568021    -0.0759092        interpolation
    7        0.563512    0.00305341        interpolation
    8        0.563686   1.09384e-05        interpolation
    9        0.563687  -1.21535e-11        interpolation
   10        0.563687  -2.88658e-15        interpolation
   11        0.563687  -2.88658e-15        interpolation
 
Zero found in the interval [1e-05, 1]
ts =
    0.5637

end


Published with MATLAB® R2015a