Unavoidable error vs. actual error

Contents

Example 1: unavoidable error

For 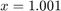$x=1.001$ compute $y=\ln x$.

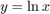The condition number is (using Taylor approximation)

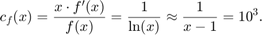
$$c_f(x)=\frac{x\cdot f'(x)}{f(x)} = \frac{1}{\ln(x)} \approx \frac{1}{x-1}=10^3.$$

Hence the unvoidable error is

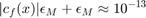
$$|c_f(x)|\epsilon_M + \epsilon_M \approx 10^{-13}$$

format compact                                 % don't print blank lines between results

x = 1.001;
cf = 1/log(x)
epsM = 1e-16;
unavoid_error = abs(cf)*epsM + epsM

cf =
          1000.49991670842
unavoid_error =
      1.00149991670842e-13

Example 1: actual error for "naive algorithm"

We compute the result yhat using yhat = log(x). We compare yhat with the value ye computed using vpa and obtain a relative error of about 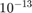$10^{-13}$.

Since the actual error is not much larger than the unavoidable error, our algorithm is numerically stable.

x = 1.001;  yhat = log(x)                      % naive evaluation result
xe = vpa('1001/1000');  ye = vpa(log(xe))      % extra precision result
actual_error = double((yhat-ye)/ye)            % relative error of yhat

yhat =
      0.000999500333083423
ye =
0.00099950033308353316680939892053501
actual_error =
     -1.10011244409463e-13

Example 2: unavoidable error

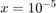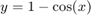For $x=10^{-5}$ compute $y=1-\cos(x)$.

The condition number is (using Taylor approximation)

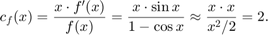
$$c_f(x)=\frac{x\cdot f'(x)}{f(x)} = \frac{x\cdot\sin x}{1-\cos x} \approx \frac{x\cdot x}{x^2/2}=2.$$

Hence the unvoidable error is

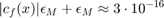
$$|c_f(x)|\epsilon_M + \epsilon_M \approx 3\cdot 10^{-16}$$

x = 1e-5;
cf = x*sin(x)/(1-cos(x))
epsM = 1e-16;
unavoid_error = abs(cf)*epsM + epsM

cf =
          1.99999983448594
unavoid_error =
      2.99999983448594e-16

Example 2: actual error for "naive algorithm"

We compute the result yhat using yhat = 1-cos(x). We compare yhat with the value ye computed using vpa and obtain a relative error of about 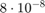$8\cdot 10^{-8}$.

Since the actual error is much larger than the unavoidable error, our algorithm is numerically unstable.

x = 1e-5;  yhat = 1-cos(x)                     % naive evaluation result
xe = vpa('10^-5');  ye = vpa(1-cos(xe))        % extra precision result
relerr = double((yhat-ye)/ye)                  % relative error of yhat

yhat =
      5.00000041370185e-11
ye =
0.000000000049999999999583333333334722222277
relerr =
      8.27487043331132e-08


Published with MATLAB® R2016b