How to compute y=1-cos(x) for x=10^(-5)

Contents

Unavoidable error

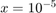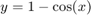For $x=10^{-5}$ compute $y=1-\cos(x)$.

The condition number is (using Taylor approximation)

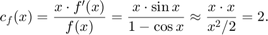
$$c_f(x)=\frac{x\cdot f'(x)}{f(x)} = \frac{x\cdot\sin x}{1-\cos x} \approx \frac{x\cdot x}{x^2/2}=2.$$

Hence the unvoidable error is

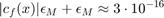
$$|c_f(x)|\epsilon_M + \epsilon_M \approx 3\cdot 10^{-16}$$

Therefore we should be able to achieve about 16 digits of accuracy in Matlab if we use a "good" algorithm.

format long g                                 % show results with 15 significant digits
x = 1e-5;
cf = x*sin(x)/(1-cos(x))
epsM = 1e-16;
unavoid_error = abs(cf)*epsM + epsM

cf =
          1.99999983448594
unavoid_error =
      2.99999983448594e-16

Algorithm 1: "Naive evaluation" of y = 1-cos(x)

We compare yhat with the extra precision value ye and obtain a relative error of about 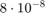$8\cdot 10^{-8}$.

Since the actual error is much larger than the unavoidable error, algorithm 1 is numerically unstable.

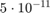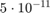Note that the computed value is larger than $5\cdot 10^{-11}$, but the correct value is less than $5\cdot 10^{-11}$.

x = 1e-5;  yhat = 1-cos(x)                     % naive evaluation result
xe = vpa('10^-5');  ye = vpa(1-cos(xe))        % extra precision result
relerr = double((yhat-ye)/ye)                  % relative error of yhat

yhat =
      5.00000041370185e-11
ye =
0.000000000049999999999583333333334722222277
relerr =
      8.27487043331132e-08

Algorithm 2: Evaluate y = sin(x)^2/(1+cos(x))

We compare yhat with extra precision value ye and obtain a relative error of about 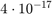$4\cdot 10^{-17}$.

Since the actual error is not much larger than the unavoidable error, algorithm 2 is numerically stable.

x = 1e-5;  yhat = sin(x)^2/(1+cos(x))          % using sin(x)^2+cos(x)^2=1
relerr = double((yhat-ye)/ye)                  % relative error of yhat

yhat =
      4.99999999995833e-11
relerr =
      4.20819139632208e-17

Algorithm 3: Evaluate y = 2 sin(x/2)^2

We compare yhat with the extra precision value ye and obtain a relative error of about 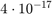$4\cdot 10^{-17}$.

Since the actual error is not much larger than the unavoidable error, algorithm 3 is numerically stable.

x = 1e-5;  yhat = 2*sin(x/2)^2                 % using formula for cos(a+b)
relerr = double((yhat-ye)/ye)                  % relative error of yhat

yhat =
      4.99999999995833e-11
relerr =
      4.20819139632208e-17

Algorithm 4: Approximate y by Taylor approximation p_3(x)

The Taylor series for f(x) = 1-cos(x) is

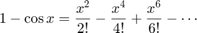
$$1-\cos x = \frac{x^2}{2!} - \frac{x^4}{4!} + \frac{x^6}{6!} - \cdots$$

We use 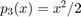$p_3(x)=x^2/2$. This introduces an approximation error: The absolute error 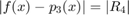$|f(x)-p_3(x)|=|R_4|$ is bounded by

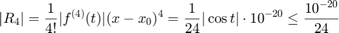
$$ |R_4| = \frac{1}{4!}|f^{(4)}(t)|(x-x_0)^4 = \frac{1}{24}|\cos t|\cdot 10^{-20}\le \frac{10^{-20}}{24}$$

the relative error 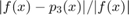$|f(x)-p_3(x)|/|f(x)|$ is therefore bounded by

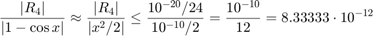
$$\frac{|R_4|}{|1-\cos x|} \approx \frac{|R_4|}{|x^2/2|} \le \frac{10^{-20}/24}{10^{-10}/2} = \frac{10^{-10}}{12}=8.33333\cdot 10^{-12}$$

We compare yhat with the extra precision value ye and obtain a relative error of about 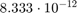$8.333\cdot 10^{-12}$ which is caused by the approximation error.

Since the actual error is much larger than the unavoidable error, algorithm 4 is numerically unstable (but it is much better than algorithm 1).

x = 1e-5;  yhat = x^2/2                        % Taylor approximation p_3(x)
relerr = double((yhat-ye)/ye)                  % relative error of yhat

yhat =
                     5e-11
relerr =
      8.33349901254303e-12

Algorithm 5: Approximate y by Taylor approximation p_5(x)

Now we use the Taylor approximation 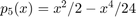$p_5(x)=x^2/2-x^4/24$. This introduces an approximation error: The absolute error 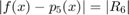$|f(x)-p_5(x)|=|R_6|$ is bounded by

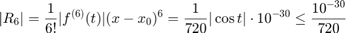
$$ |R_6| = \frac{1}{6!}|f^{(6)}(t)|(x-x_0)^6 = \frac{1}{720}|\cos t|\cdot 10^{-30}\le \frac{10^{-30}}{720}$$

the relative error 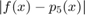$|f(x)-p_5(x)|$ is therefore bounded by

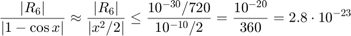
$$\frac{|R_6|}{|1-\cos x|} \approx \frac{|R_6|}{|x^2/2|} \le \frac{10^{-30}/720}{10^{-10}/2} = \frac{10^{-20}}{360}=2.8\cdot 10^{-23}$$

We compare yhat with the extra precision value ye and obtain a relative error of about 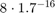$8\cdot 1.7^{-16}$.

Since the actual error is not much larger than the unavoidable error, algorithm 5 is numerically stable.

x = 1e-5;  yhat = x^2/2 - x^4/24               % Taylor approximation p_5(x)
relerr = double((yhat-ye)/ye)                  % relative error of yhat

yhat =
      4.99999999995833e-11
relerr =
      1.71328884675708e-16


Published with MATLAB® R2016b