Assignment #1, Problem 4
Contents
Solving linear system (i)
Gaussian elimination gives a matrix U with nonzero diagonal elements, hence there is a unique solution.
A = [1,2;2,1] [L,U,p] = lu(A,'vector'); U % matrix U from Gaussian elimination b = [3;4] x = A\b % unique solution
A =
1 2
2 1
U =
2 1
0 1.5
b =
3
4
x =
1.6667
0.66667
Plotting lines for linear system (ii)
The two lines intersect in a single point x which is the solution of the linear system we found before.
L1 = diag( b(1)./A(1,:) ) % two points satisfying eq.1 L2 = diag( b(2)./A(2,:) ) % two points satisfying eq.2 plotpoints(L1); hold on % plot line for eq.1 plotpoints(L2,'--') % plot line for eq.2 plotpoints(x,'ko'); label(x,'x') % plot solution point hold off axis equal; grid on; title('Two lines intersect at solution point x') legend('equation 1','equation 2')
L1 =
3 0
0 1.5
L2 =
2 0
0 4

Solving linear system (ii)
Gaussian elimination fails, it does not give matrix U with nonzero diagonal elements. Hence the matrix A is singular. So the linear system has either no solution or infinitely many solutions.
Using \ with machine arithmetic gives a warning that the matrix is singular within machine precision.
Using \ with symbolic arrays gives a message that no solution exists.
A = [1,2;2,4] [L,U,p] = lu(A,'vector'); U % matrix U from Gaussian elimination b = [3;4] % Using Matlab with machine arithmetic x = A\b % Matlab gives Inf (infinity) % Using symbolic computation: x = sym(A)\sym(b) % symbolic \ gives warning that no solution exists
A =
1 2
2 4
U =
2 4
0 0
b =
3
4
Warning: Matrix is singular to working precision.
x =
Inf
-Inf
Warning: The system is inconsistent. Solution does not exist.
x =
Inf
Inf
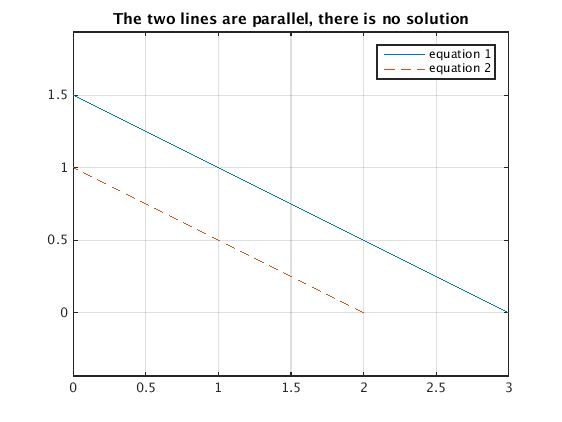
Plotting lines for linear system (ii)
Here the two lines are parallel and do not intersect since the linear system has no solution.
L1 = diag( b(1)./A(1,:) ) % two points satisfying eq.1 L2 = diag( b(2)./A(2,:) ) % two points satisfying eq.2 plotpoints(L1); hold on % plot line for eq.1 plotpoints(L2,'--'); hold off % plot line for eq.2 axis equal; grid on; title('The two lines are parallel, there is no solution') legend('equation 1','equation 2')
L1 =
3 0
0 1.5
L2 =
2 0
0 1
Solving linear system (iii)
Since A is singular there is either no solution or infinitely many solutions.
Note that the backslash command in machine arithmetic gives a warning "matrix is singular to working precision". But it does not return any solution (despite the fact that there are solutions).
Using symbolic computation in Matlab we obtain a particular solution xpart, and a basis V for the null space (one vector). Hence the solution is given by a line xpart+t*V with arbitrary t.
b = [3;6] % Using Matlab with machine arithmetic x = A\b % Matlab gives NaN (not a number) % Using symbolic computation: xpart = sym(A)\sym(b) % symbolic \ gives one solution and % warning that more solutions exist V = null(sym(A)) % basis for null space
b =
3
6
Warning: Matrix is singular to working precision.
x =
NaN
NaN
Warning: The system is rank-deficient. Solution is not unique.
xpart =
3
0
V =
-2
1
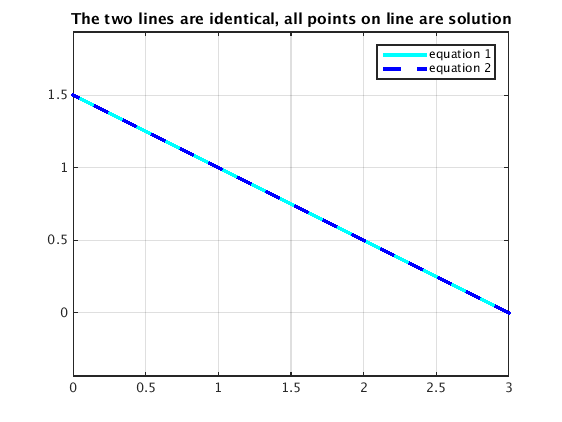
Plotting lines for linear system (iii)
Here the two lines are parallel and do not intersect since the linear system has no solution.
L1 = diag( b(1)./A(1,:) ) % two points satisfying eq.1 L2 = diag( b(2)./A(2,:) ) % two points satisfying eq.2 plotpoints(L1,'c','LineWidth',3); hold on % plot line for eq.1 plotpoints(L2,'b--','LineWidth',3); hold off % plot line for eq.2 axis equal; grid on; title('The two lines are identical, all points on line are solution') legend('equation 1','equation 2')
L1 =
3 0
0 1.5
L2 =
3 0
0 1.5