Solving the Poisson Equation (Dirichlet case) using the Discrete Sine Transform

Contents

You first have to download m-files

Download the m-files sintr.m , isintr.m and put them in the same directory as your other m-files.

Solve the Poisson equation 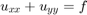$u_{xx} + u_{yy} = f$ in a rectangle

We are given a "forcing function" 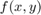$f(x,y)$ for $x\in [0,A]$, $y\in[0,B]$. We want to find a function $u(x,y)$ for $x\in [0,A]$, $y\in[0,B]$ such that

$$u_{xx}(x,y) + u_{yy}(x,y) = f(x,y) \qquad x\in (0,A)$, $y\in(0,B) \quad\mbox{(PDE)}$$

We prescribe Dirichlet boundary conditions on all four sides of the rectangle:

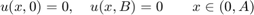
$$ u(x,0) = 0 , \quad u(x,B) = 0 \qquad x\in (0,A)$$

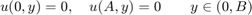
$$ u(0,y) = 0 , \quad u(A,y) = 0 \qquad y\in (0,B)$$

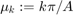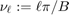
We write the solution $u(x,y)$ as a sine series for both x and y: With $\mu_k:=k\pi/A$ and $\nu_\ell:=\ell\pi/B$

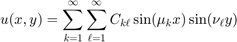
$$ u(x,y) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty C_{k\ell} \sin(\mu_k x)\sin(\nu_\ell y)$$

From this we get

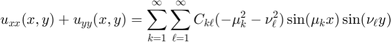
$$ u_{xx}(x,y) + u_{yy}(x,y) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty C_{k\ell} (-\mu_k^2-\nu_\ell^2)\sin(\mu_k x)\sin(\nu_\ell y)$$

This gives the following Solution Formula: First find the sine series of 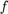$f$ for both x and y:

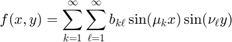
$$ f(x,y) = \sum_{k=1}^\infty \sum_{\ell=1}^\infty b_{k\ell} \sin(\mu_k x)\sin(\nu_\ell y)$$

Define for 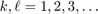$k,\ell=1,2,3,\ldots$ the coefficients 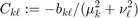$\displaystyle C_{k\ell} := -b_{k\ell}/(\mu_k^2+\nu_\ell^2)$, then the solution $u(x,y)$ is given by the above sine series in x,y.

Example: For a rectangle with lengths 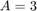$A=3$ and $B=2$ we are given the forcing function $f(x,y)=x(x-3)+y(y-2)$.

A=3; B=2;                       % lengths of rectangle sides
f = @(x,y) x.*(x-A)+y.*(y-B);   % given forcing function f(x,y)

M = 60;                         % use spacing A/M for x
x = A*(1:M-1)/M;                % only interior nodes
N = 40;                         % use spacing B/N for y
y = B*(1:N-1)/N;                % only interior nodes

[X,Y] = ndgrid(x,y);
F = f(X,Y);                     % F is array of values of f on grid:  F(j,k) = f(x_j,y_k)
bx = sintr(F);                  % apply sine transform to columns
b = sintr(bx')';                % apply sine transform to rows

mu = (1:M-1)*pi/A;              % vector of mu_k
nu = (1:N-1)*pi/B;              % vector of nu_l
[Mu,Nu] = ndgrid(mu,nu);

C = -b./(Mu.^2+Nu.^2);          % solution formula in frequency domain

Cx = isintr(C')';               % apply inverse sine transform to rows
U = isintr(Cx);                 % apply inverse sine transform to columns

surf(x,y,U');                   % make surface plot of solution
xlabel('x'); ylabel('y'); title('u(x,y)')
view(-15,30);

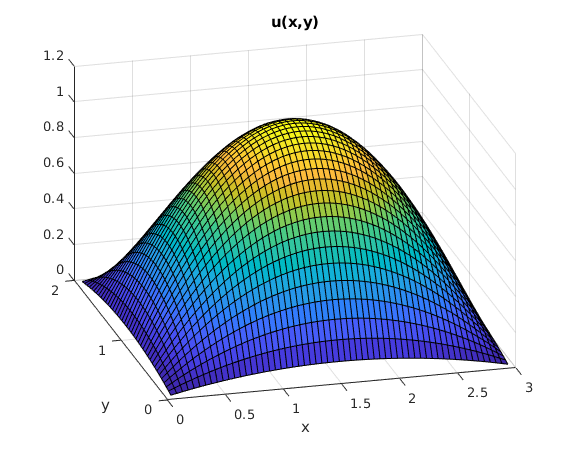
Plot error

In this case we actually know the exact solution 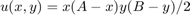$u(x,y)=x(A-x)y(B-y)/2$. We can plot the difference of the computed solution and the exact solution, and we see that the error is of the order 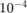$10^{-4}$. We can decrease the error by using higher values of $M,N$.

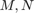Uex = X.*(A-X).*Y.*(B-Y)/2;           % evaluate exact solution on grid
surf(x,y,(U-Uex)');                   % make surface plot of U-Uex
xlabel('x'); ylabel('y'); title('error')
view(-15,30);


Published with MATLAB® R2018a