Solution Assignment 2 (MATH464, Spring 2020)
Contents
You need to download an m-file
Download the m-file foursum.m. Put it in the same folder as your other m-files.
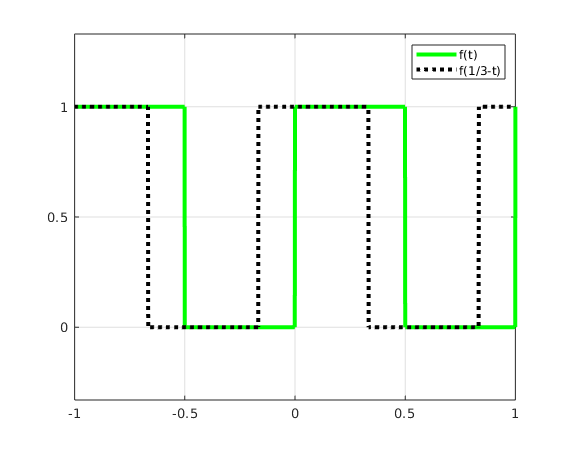
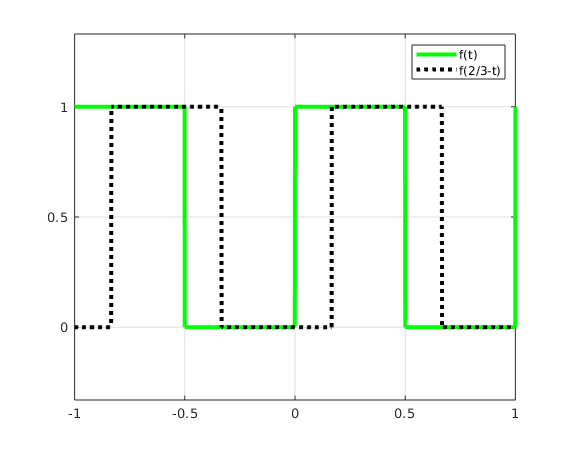
1(a) Sketch graphs of f(t) and f(1/3-t), graphs of f(t) and f(2/3-t)
(The vertical lines are not really part of the graphs.)
format compact; format short g frac = @(x) x-floor(x); % fractional part f = @(x) frac(x)<.5; % define function f t = -1:.001:1; plot(t,f(t),'g',t,f(1/3-t),'k:','LineWidth',3); axis equal grid on; xticks(-1:.5:1); yticks(-1:.5:1); legend('f(t)','f(1/3-t)') snapnow plot(t,f(t),'g',t,f(2/3-t),'k:','LineWidth',3); axis equal; grid on; xticks(-1:.5:1); yticks(-1:.5:1); legend('f(t)','f(2/3-t)')
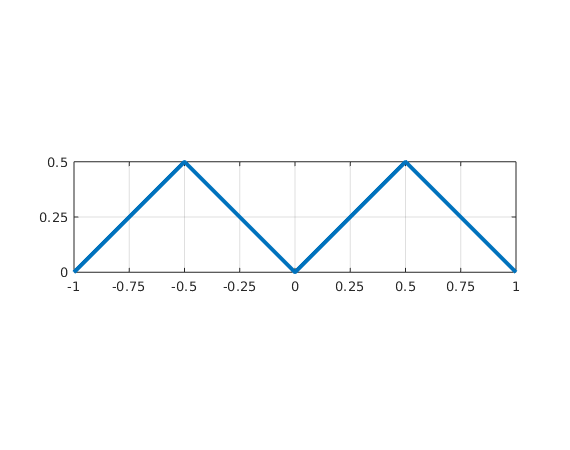
1(a)(iii) Sketch graph of q(x) on [-1,1]
We found: q(x) is 1-periodic function with
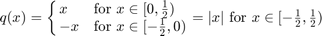
x = linspace(-1,1,1000); q = abs(x-round(x)); plot(x,q,'LineWidth',3); xticks(-1:.25:1); yticks(0:.25:.5); axis equal; axis([-1 1 0 .5]); grid on
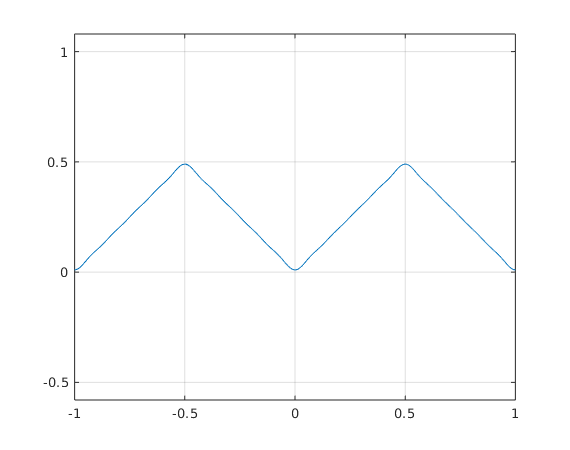
1(b) Plot 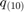 for convolution q=f*f
for convolution q=f*f
Note that 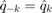 .
.
nv = 1:10; % vector of frequencies qhpos = -1./(pi^2*nv.^2); % vector qhpos = [qhat_1,...,qhat_{10}] qhpos(2:2:end) = 0; % set to zero for even k x = linspace(-1,1,1000); % 1000 equidistant points from -1 to 1 for plotting plot(x,foursum(x,.25,qhpos)); grid on; axis equal
Warning: Imaginary parts of complex X and/or Y arguments ignored
2(b) Plot  for h=1/8
for h=1/8
Note 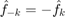 ,
, 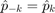 .
.
h = 1/8; nv = 1:30; fh0 = .5; fhpos = -1i./(pi*nv); % vector fhpos = [qhat_1,...,qhat_{10}] fhpos(2:2:end) = 0; % set to zero for even k ph0 = 1; phpos = sinc(nv*h); % NOTE: sinc_Matlab(x) = sinc(pi*x) x = linspace(-1,1,1000); % 1000 equidistant points from -1 to 1 for plotting plot(x,foursum(x,fh0*ph0,fhpos.*phpos)); grid on; title('f{\ast}p')
Warning: Imaginary parts of complex X and/or Y arguments ignored
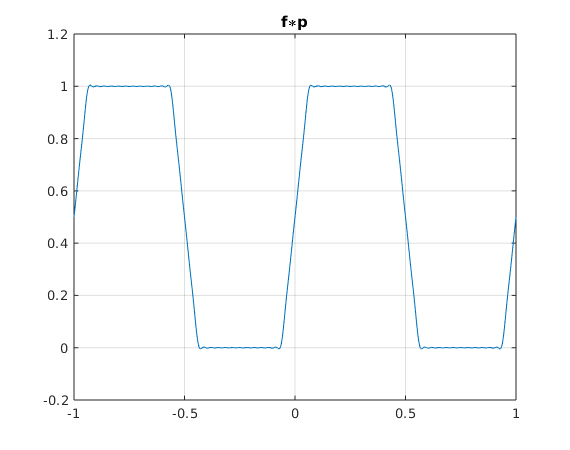
2(b) Plot 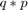
Note 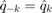 ,
, 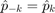 .
.
qh0 = fh0*fh0; qhpos = fhpos.*fhpos; plot(x,foursum(x,qh0*ph0,qhpos.*phpos)); grid on; title('q{\ast}p')
Warning: Imaginary parts of complex X and/or Y arguments ignored
4(a)
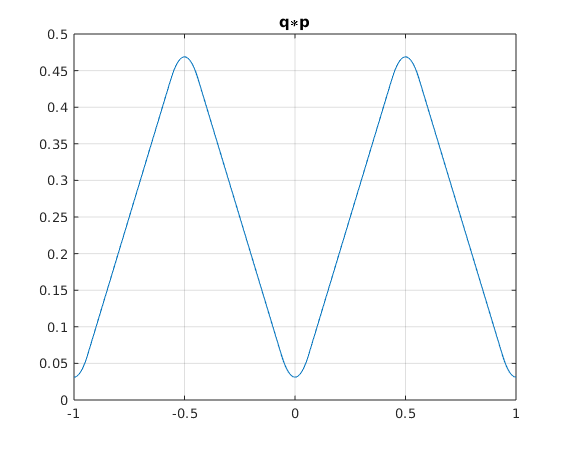
Consider 1-periodic functions 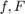 with
with 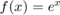 and
and 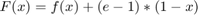 for
for ![$x\in[0,1]$](a2sol_eq00029426888847692995.png) .
.
x = (0:999)/1000; f = exp(x); F = f + (exp(1)-1)*(1-x); plot([x-1,x],[f,f],[x-1,x],[F,F]) legend('f','F','Location','SouthEast')
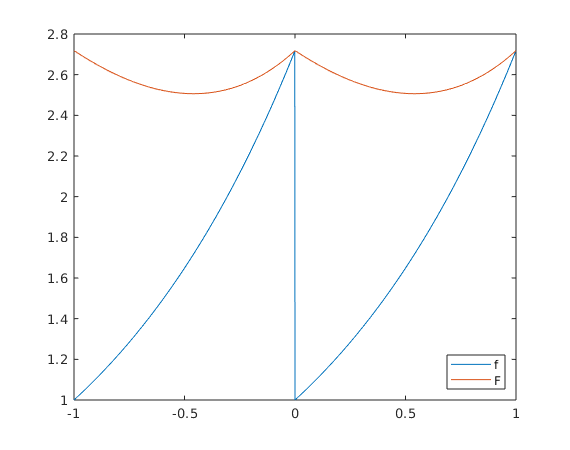
4(c),(d) Plot 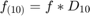 together with
together with 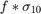
We have
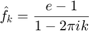
N = 10; Nv = 1:N; c = exp(1) - 1; fh0 = c; fhpos = c./(1-2i*pi*Nv); shpos = (1-Nv/(N+1)); % f*sigma10: fhat_k*(1-|k|/(N+1)) qhpos = sinc(Nv/(N+.5)); % f*A10: fhat_k*sinc_Matlab(k/(N+.5)) x = 0:.001:1; plot(x,foursum(x,fh0,fhpos),x,foursum(x,fh0,fhpos.*shpos),... x,foursum(x,fh0,fhpos.*qhpos),x,exp(x),'k:') legend('f_{(10)}','f*\sigma_{10}','f*A_{10}','f','Location','NorthWest') snapnow x = 0:.001:.5; f = exp(x); plot(x,foursum(x,fh0,fhpos)-f,x,foursum(x,fh0,fhpos.*shpos)-f,... x,foursum(x,fh0,fhpos.*qhpos)-f) grid on; axis tight; title('errors') legend('f_{(10)}-f','f*\sigma_{10}-f','f*A_{10}-f')
Warning: Imaginary parts of complex X and/or Y arguments ignored
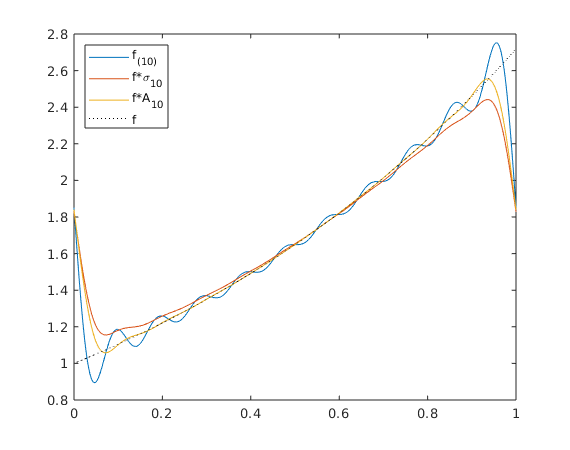
Warning: Imaginary parts of complex X and/or Y arguments ignored
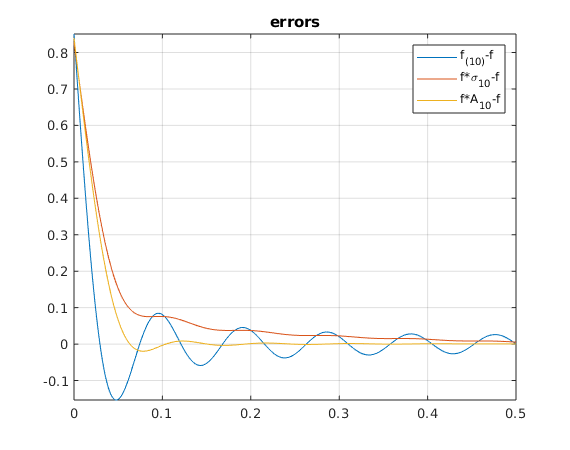
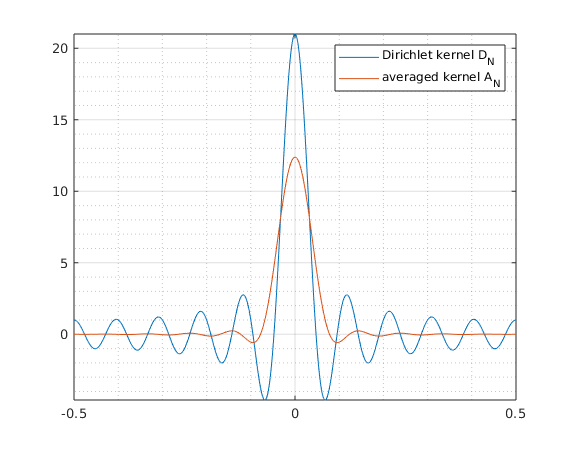
4(d) Plot Dirichlet kernel 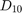 , kernel
, kernel 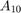
For 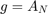 we have the Fourier coefficients
we have the Fourier coefficients 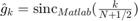 for
for 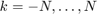 ,
, 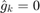 for
for 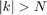 .
.
Note that for ![$x\in[.25,.75]$](a2sol_eq06322394059567932196.png) we have
we have 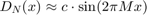 with
with 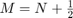 . Therefore
. Therefore 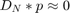 in [.25,.75], see problem 3(i).
in [.25,.75], see problem 3(i).
x = -.5:.001:.5; plot(x,foursum(x,1,Nv.^0),x,foursum(x,1,qhpos)); axis tight; grid on; grid minor legend('Dirichlet kernel D_N','averaged kernel A_N')
Warning: Imaginary parts of complex X and/or Y arguments ignored