Approximating the continuous Fourier transform fhat(xi) using the discrete Fourier transform (FFT)
Contents
You need to download some m-files
Download the following m-files and put them in the same directory with your other m-files:
format compact % don't print blank lines between results
Define f(x) and find Fourier transform fhat(xi)
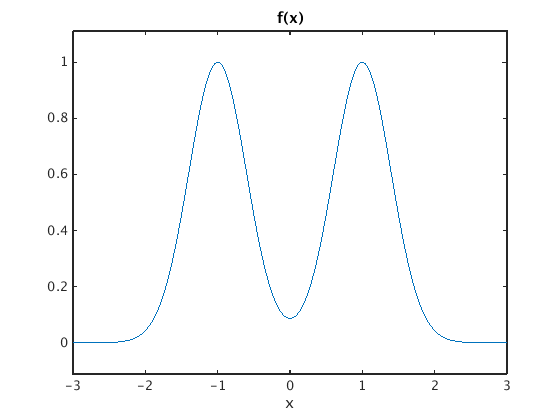
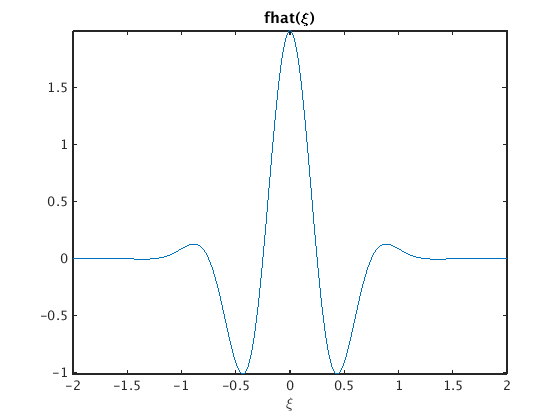
syms x xi % set up symbolic variables Pi = sym('pi'); % and symbolic pi f = exp(-Pi*(x-1)^2) + exp(-Pi*(x+1)^2) fhat = simple(Four(f,x,xi)) % find Fourier transform and simplify figure(1); ezplot(f,[-3,3]); title('f(x)') % plot f figure(2); ezplot(fhat,[-2,2]); axis tight % plot fhat title('fhat(\xi)')
f = exp(-pi*(x - 1)^2) + exp(-pi*(x + 1)^2) fhat = 2*exp(-pi*xi^2)*cos(2*pi*xi)
Take samples g_j = f(jh) for j=-M...M
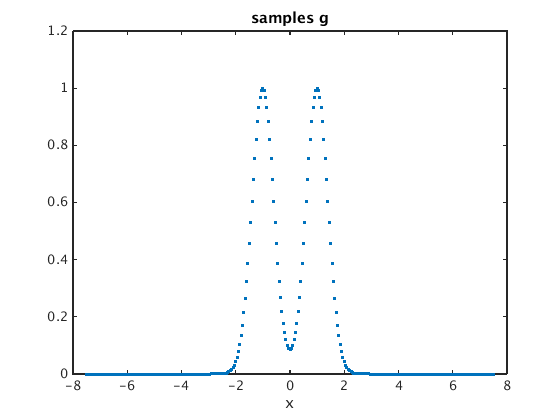
h = 0.05; % spacing M = 150; N = 2*M+1; % number of values X = (-M:M)*h; % discrete x values g = exp(-pi*(X-1).^2) + exp(-pi*(X+1).^2); % samples of f plot(X,g,'.') % plot samples xlabel('x'); title('samples g')
Find discrete Fourier transform
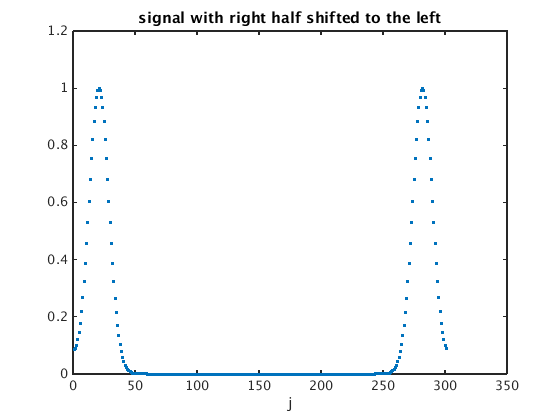
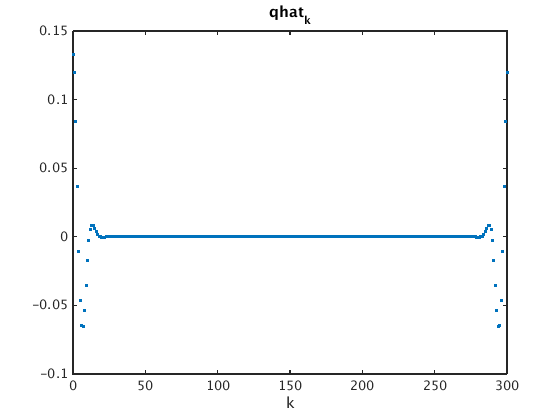
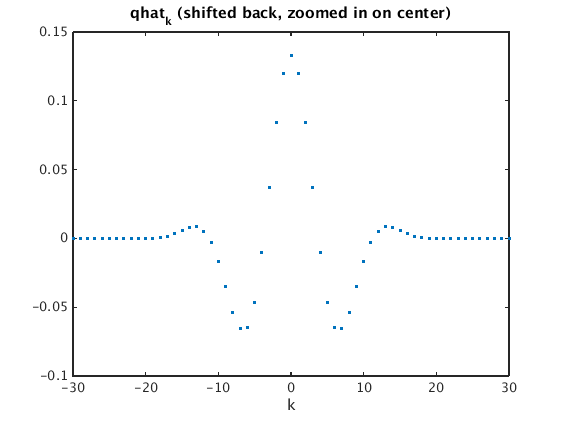
gs = ifftshift(g); % shift left half of signal to the right figure(1); plot(gs,'.'); xlabel('j'); title('signal with right half shifted to the left') qhat = four(gs); figure(2); plot(0:N-1,qhat,'.'); xlabel('k'); title('qhat_k') qhats = fftshift(qhat); % shift right half to the left figure(3); plot(-M:M,qhats,'.'); xlim([-30 30]); xlabel('k') % show -30...30 on horizontal axis title('qhat_k (shifted back, zoomed in on center)')
How is qhat related to fhat?
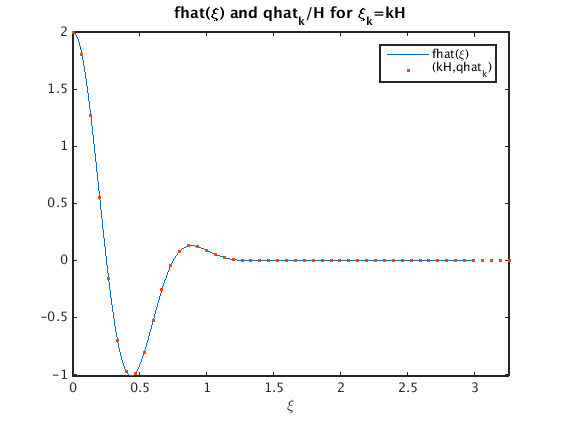
Answer: for H = 1/(N*h) we have that qhat_k/H approximates fhat(k*H)
H = 1/(N*h); % spacing in frequency domain ezplot(fhat,[0,3]); hold on % plot fhat plot((0:49)*H,qhat(1:50)/H,'.'); % plot points (k*H,qhat_k) hold off; axis tight title('fhat(\xi) and qhat_k/H for \xi_k=kH') legend('fhat(\xi)','(kH,qhat_k)')