Evaluating finite Fourier series using foursum

Contents

You need to download an m-file

Download the m-file foursum.m. Put it in the same folder as your other m-files.

Approximating a function using finite Fourier sums

A 1-periodic function 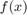$f(x)$ has a Fourier series

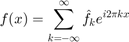
$$ f(x) = \sum_{k=-\infty}^\infty \hat f_k e^{i2\pi k x}$$

We can approximate this by computing a FINITE sum

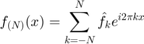
$$ f_{(N)}(x) = \sum_{k=-N}^N \hat f_k e^{i2\pi k x}$$

As 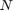$N$ increases this should converge to the function $f(x)$.

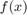Example 1: 1-periodic function with f(x) = x on [0,1], sum over k=-10...10

Here the Fourier coefficients are

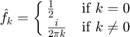
$$\hat{f}_k = \cases{ \frac{1}{2} & if $k=0$ \cr \frac{i}{2\pi k} & if $k\ne 0$ }$$

Note that the function is real-valued, and we have 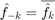$\hat f_{-k}=\overline{\hat f_{k}}$. We can therefore omit the argument fhneg of foursum, and foursum will use fhneg=conj(fhpos).

N = 10;                      % use frequencies up to N
nv = 1:N;                    % vector [1,2,...,N] of frequencies
fhpos = 1i./(2*pi*nv);       % vector [fhat_1,...,fhat_N] for positive k

x = linspace(-1,1,1000);     % 1000 equidistant points from -1 to 1 for plotting
plot(x,foursum(x,.5,fhpos)); grid on

Warning: Imaginary parts of complex X and/or Y arguments ignored

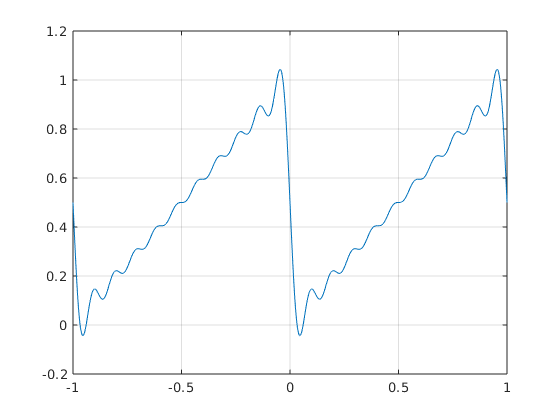
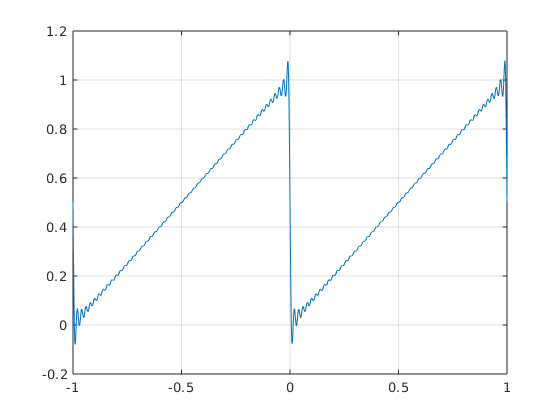
sum over k=-50...50

N = 50;                      % use frequencies up to N
nv = 1:N;                    % vector [1,2,...,N] of frequencies
fhpos = 1i./(2*pi*nv);       % vector [fhat_1,...,fhat_N] for positive k

x = linspace(-1,1,1000);     % 1000 equidistant points from -1 to 1 for plotting
plot(x,foursum(x,.5,fhpos)); grid on

Warning: Imaginary parts of complex X and/or Y arguments ignored

Example 2: 1-periodic function which is 1 on [0,.5) and -1 on [-.5,0), sum over k=-10...10

Here the Fourier coefficients are

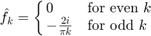
$$\hat{f}_k = \cases{ 0 & for even $k$ \cr -\frac{2i}{\pi k} & for odd $k$ }$$

Note that the function is real-valued. Hence we have 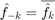$\hat f_{-k}=\overline{\hat f_{k}}$ and we can therefore omit the argument fhneg of foursum.

N = 10;                      % use frequencies up to N
nv = 1:N;                    % vector [1,2,...,N] of frequencies
fhpos = -2i./(pi*nv);        % vector [fhat_1,...,fhat_N] for positive k
fhpos(2:2:end) = 0;          % set even components of fhpos to zero

x = linspace(-1,1,1000);     % 1000 equidistant points from -1 to 1 for plotting
plot(x,foursum(x,0,fhpos)); grid on

Warning: Imaginary parts of complex X and/or Y arguments ignored

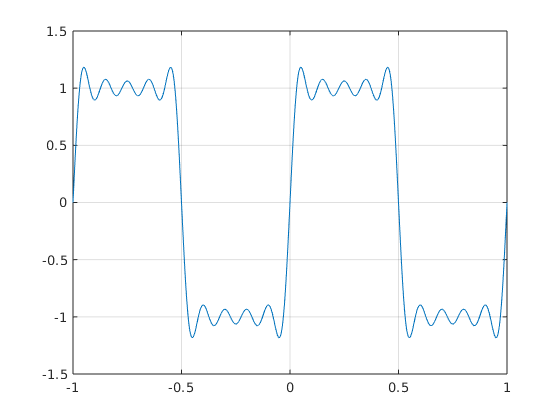
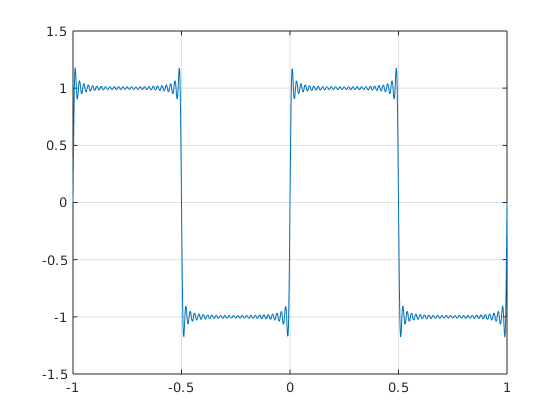
sum over k=-50...50

N = 50;                      % use frequencies up to N
nv = 1:N;                    % vector [1,2,...,N] of frequencies
fhpos = -2i./(pi*nv);        % vector [fhat_1,...,fhat_N] for positive k
fhpos(2:2:end) = 0;          % set even components of fhpos to zero

x = linspace(-1,1,1000);     % 1000 equidistant points from -1 to 1 for plotting
plot(x,foursum(x,0,fhpos)); grid on

Warning: Imaginary parts of complex X and/or Y arguments ignored


Published with MATLAB® R2019b